【题目】已知：如图，四边形ABCD是菱形，点G是BC延长线上一点，连接AG，分别交BD、CD于点E、F，连接CE。

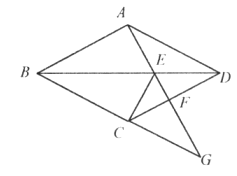
（1）求证：∠DAE＝∠DCE； （2）求证：AE2＝EF·EG。

参考答案：

【答案】（1）、证明过程见解析；（2）、证明过程见解析

【解析】

试题分析：（1）、根据菱形的性质得出△ADE和△CDE全等，从而得出答案；（2）、根据菱形的性质得出∠DAG＝∠G，根据已知条件得出∠DCE＝∠G，从而得出△ECF和△EGC相似，结合△ADE和△CDE得出答案.

试题解析：（1）、∵四边形ABCD是菱形 ，AB∥CD ∴∠ABD＝∠ADB，∠ABD＝∠CDE，

∴∠ADE＝∠CDE，AD＝CD ∴△ADE≌△CDE（SAS） ∴∠DAE＝∠DCE

（2）、∵四边形ABCD是菱形 ∴AD∥BC，∠DAG＝∠G ∵∠DAE＝∠DCE ∴∠DCE＝∠G

∵∠CEF＝∠GEC ∴△ECF∽△EGC ∵△ADE≌△CDE，

关闭