
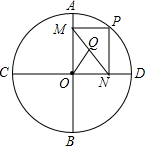
 如图,⊙O的半径为2,AB、CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A、B、C、D不重合),经过P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,线段OQ所扫过过的面积为( )
如图,⊙O的半径为2,AB、CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A、B、C、D不重合),经过P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,线段OQ所扫过过的面积为( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{8}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{4}$ |
分析 由于OP的长度不变,始终等于半径,则根据矩形的性质可得OQ=1,再由走过的角度代入弧长公式求得点Q走过的路径长,入会根据扇形的面积公式即可得到结论.
解答 解:∵PM⊥AB于点M,PN⊥CD于点N,
∴四边形ONPM是矩形,
又∵点Q为MN的中点,
∴点Q为OP的中点,
则OQ=1,
点Q走过的路径长=$\frac{45π×1}{180}$=$\frac{π}{4}$.
∴线段OQ所扫过过的面积=$\frac{1}{2}×\frac{π}{4}$×1=$\frac{π}{8}$,
故选B.
点评 本题考查了扇形的面积的计算,弧长的计算,矩形的性质,解答本题的关键是根据矩形的性质得出点Q运动轨迹的半径,要求同学们熟练掌握弧长的计算公式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 明天A地区80%的时间都下雨 | B. | 明天A地区的降雨量是同期的80% | ||
| C. | 明天A地区80%的地方都下雨 | D. | 明天A地区下雨的可能性是80% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{5}$ | C. | $\sqrt{4}$ | D. | $\sqrt{0.8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com