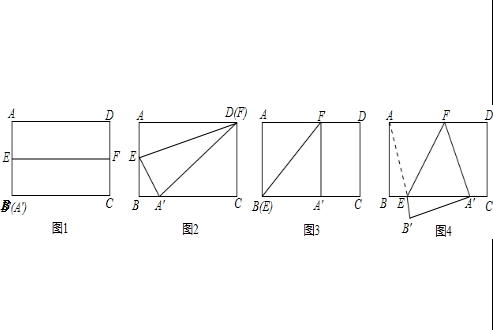
解:(1)当A′与B重合时,如图1,把矩形对折,所以EF=AD=5.
故答案为5;
如图2,DC=AB=3,A′F=AD=5,
在Rt△A′CF中,A′C=

=4,
设AE=t,则BE=3-t,EA′=t,
在Rt△EBA′中,BA′=BC-A′C=5-4=1,
∵BE
2+BA′
2=EA′
2,
∴(3-t)
2+1
2=t
2,解得t=

,
在RtAEF中,AE=

,AF=5,
∴EF=

=
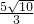
;
(2)①3≤x≤5;
②如图4,∵△AEF沿EF折叠到△A′EF,
∴EA=EA′,FA=FA′,∠AEF=∠A′EF,
∵四边形ABCD为矩形,
∴AF∥EC,
∴∠A′EF=∠AFE,
∴∠A′FE=∠A′EF,
∴A′E=A′F,
∴AE=EA′=A′F=FA,
∴四边形AEA′F是菱形.
分析:(1)由于矩形对折,于是EF=AD=5;根据折叠的性质得到DC=AB=3,A′F=AD=5,在Rt△A′CF中利用勾股定理可计算出A′C=4,设AE=t,则BE=3-t,EA′=t,在Rt△EBA′中,利用勾股定理得(3-t)
2+1
2=t
2,解得t=

,然后在RtAEF中,利用勾股定理即可计算出EF;
(2)①当折痕FE过B点时,四边形AEA′F是正方形,BA′最小,此时BA′=BA=3;当点A的对应点A′落在C点时,BA′=5,于是得到x的取值范围是3≤x≤5,四边形AEA′F是菱形;
②根据折叠的性质得到EA=EA′,FA=FA′,∠AEF=∠A′EF,根据平行线的性质可得∠A′EF=∠AFE,则有∠A′FE=∠A′EF,于是A′E=A′F,易得AE=EA′=A′F=FA,根据菱形的判定即可得到结论.
点评:本题考查了折叠的性质:折叠前后两图形全等,折痕垂直平分对应点的连线段.也考查了矩形的性质、勾股定理以及菱形的判定与性质.

 =4,
=4, ,
, ,AF=5,
,AF=5, =
=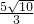 ;
; ,然后在RtAEF中,利用勾股定理即可计算出EF;
,然后在RtAEF中,利用勾股定理即可计算出EF;

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案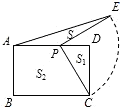 在矩形ABCD中,AD=4,点P在AD上,且AP:PD=a:b
在矩形ABCD中,AD=4,点P在AD上,且AP:PD=a:b 如图,矩形ABCD中,AD=2,AB=3,AM=1,
如图,矩形ABCD中,AD=2,AB=3,AM=1,
