
【题目】已知正方形ABCD,E为平面内任意一点,连结DE,将线段DE绕点D顺时针旋转90°得到DG,连结EC,AG.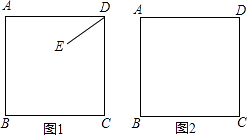
(1)当点E在正方形ABCD内部时,
①依题意补全图形;
②判断AG与CE的数量关系与位置关系并写出证明思路.
(2)当点B,D,G在一条直线时,若AD=4,DG= ![]() ,求CE的长.
,求CE的长.
【答案】
(1)
证明:①依题意补全图形,如图1所示,

②AG=CE,AG⊥CE.
证明思路如下:

由正方形ABCD,可得AD=CD,∠ADC=90°,
由DE绕着点D顺时针旋转90°得DG,
∴∠GDE=∠ADC=90°,GD=DE
∴∠GDA=∠EDC.
∵DG=DE,AD=CD,
∴△AGD≌△CED,
∴AG=CE.
延长CE分别交AG、AD于点F、H,
∵△AGD≌△CED,
∴∠GAD=∠ECD,
∵∠AHF=∠CHD,
∴∠AFH=∠HDC=90°
∴AG⊥CH
(2)
证明:当点G在线段BD的延长线上时,如图3所示.

过G作GM⊥AD于M.
∵BD是正方形ABCD的对角线,
∴∠ADB=∠GDM=45°.
∵GM⊥AD,DG= ![]() ,
,
∴MD=MG=1
在Rt△AMG中,由勾股定理,得AG= ![]() =
= ![]()
∴CE=AG= ![]()
当点G在线段BD上时,如图4所示.

过G作GM⊥AD于M.
∵BD是正方形ABCD的对角线,
∴∠ADG=45°
∵GM⊥AD,DG= ![]() ,
,
∴MD=MG=1
在Rt△AMG中,由勾股定理,得AG= ![]() =
= ![]() ,
,
∴CE=AG= ![]()
故CE的长为 ![]() 或
或 ![]()
【解析】(1)依题意补全图形,如图1所示,(2)由旋转得到∠GDA=∠EDC,判断出△AGD≌△CED,得出∠AFH=∠HDC=90°即可;(3)由正方形的线段得到MD=MG=1,再根据勾股定理计算即可.
【考点精析】本题主要考查了图形的旋转的相关知识点,需要掌握每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在正△ABC中,D、E分别在AC、AB上,且 ![]() =
= ![]() , AE=BE , 则有( )
, AE=BE , 则有( ) 
A.△AED∽△ABC
B.△ADB∽△BED
C.△BCD∽△ABC
D.△AED∽△CBD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
根据联合国《人口老龄化及其社会经济后果》中提到的标准,当一个国家或地区65 岁及以上老年人口数量占总人口比例超过7%时,意味着这个国家或地区进入老龄化.从经济角度,一般可用“老年人口抚养比”来反映人口老龄化社会的后果.所谓“老年人口抚养比”是指某范围人口中,老年人口数(65 岁及以上人口数)与劳动年龄人口数(15﹣64 岁人口数)之比,通常用百分比表示,用以表明每100 名劳动年龄人口要负担多少名老年人.
以下是根据我国近几年的人口相关数据制作的统计图和统计表.
2011﹣2014 年全国人口年龄分布图
2011﹣2014 年全国人口年龄分布表
2011年 | 2012年 | 2013年 | 2014年 | |
0﹣14岁人口占总人口的百分比 | 16.4% | 16.5% | 16.4% | 16.5% |
15﹣64岁人口占总人口的百分比 | 74.5% | 74.1% | 73.9% | 73.5% |
65岁及以上人口占总人口的百分比 | m | 9.4% | 9.7% | 10.0% |
根据以上材料解答下列问题:
(1)2011 年末,我国总人口约为亿,全国人口年龄分布表中m的值为;
(2)若按目前我国的人口自然增长率推测,到2027 年末我国约有14.60 亿人.假设0﹣14岁人口占总人口的百分比一直稳定在16.5%,15﹣64岁人口一直稳定在10 亿,那么2027 年末我国0﹣14岁人口约为亿,“老年人口抚养比”约为;(精确到1%)
(3)2016 年1 月1 日起我国开始实施“全面二胎”政策,一对夫妻可生育两个孩子,在未来10年内,假设出生率显著提高,这(填“会”或“不会”)对我国的“老年人口抚养比”产生影响.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=120°,BD平分∠ABC,∠DAC=60°,若AB=2,BC=3,则BD的长是( )

A. 5 B. 7 C. 8 D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数 ![]() 与反比例函数
与反比例函数 ![]() 的图象在第一象限的交点为A(1,n).
的图象在第一象限的交点为A(1,n). 
(1)求m与n的值;
(2)设一次函数的图象与x轴交于点B,连结OA,求∠BAO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF. 
(1)求证:四边形BFDE是矩形.
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设在一个变化过程中有两个变量x与y,如果对于x的每一个值,y都有唯一确定的值和它对应,那么就说y是x的函数,记作y=f(x).在函数y=f(x)中,当自变量x=a时,相应的函数值y可以表示为f(a).
例如:函数f(x)=x2﹣2x﹣3,当x=4时,f(4)=42﹣2×4﹣3=5在平面直角坐标系xOy中,对于函数的零点给出如下定义:
如果函数y=f(x)在a≤x≤b的范围内对应的图象是一条连续不断的曲线,并且f(a).f(b)<0,那么函数y=f(x)在a≤x≤b的范围内有零点,即存在c(a≤c≤b),使f(c)=0,则c叫做这个函数的零点,c也是方程f(x)=0在a≤x≤b范围内的根.
例如:二次函数f(x)=x2﹣2x﹣3的图象如图1所示.
观察可知:f(﹣2)>0,f(1)<0,则f(﹣2).f(1)<0.所以函数f(x)=x2﹣2x﹣3在﹣2≤x≤1范围内有零点.由于f(﹣1)=0,所以,﹣1是f(x)=x2﹣2x﹣3的零点,﹣1也是方程x2﹣2x﹣3=0的根.
(1)观察函数y1=f(x)的图象2,回答下列问题:
①f(a)f(b) 0(“<”“>”或“=”)
②在a≤x≤b范围内y1=f(x)的零点的个数是 .
(2)已知函数y2=f(x)=﹣ ![]() 的零点为x1 , x2 , 且x1<1<x2 .
的零点为x1 , x2 , 且x1<1<x2 .
①求零点为x1 , x2(用a表示);
②在平面直角坐标xOy中,在x轴上A,B两点表示的数是零点x1 , x2 , 点 P为线段AB上的一个动点(P点与A、B两点不重合),在x轴上方作等边△APM和等边△BPN,记线段MN的中点为Q,若a是整数,求抛物线y2的表达式并直接写出线段PQ长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】表是二次函数y=ax2+bx+c的部分x,y的对应值:
x | … | ﹣1 | ﹣ | 0 |
| 1 |
| 2 |
| 3 | … |
y | … | m |
| ﹣1 |
| ﹣2 |
| ﹣1 |
| 2 | … |
(1)二次函数图象的开口向 , 顶点坐标是 , m的值为;
(2)当x>0时,y的取值范围是;
(3)当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时,n的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+3(a≠0)的图象经过点A(3,0),B(4,1),且与y轴交于点C,连接AB、AC、BC.
(1)求此二次函数的关系式;
(2)判断△ABC的形状;若△ABC的外接圆记为⊙M,请直接写出圆心M的坐标;
(3)若将抛物线沿射线BA方向平移,平移后点A、B、C的对应点分别记为点A1、B1、C1 , △A1B1C1的外接圆记为⊙M1 , 是否存在某个位置,使⊙M1经过原点?若存在,求出此时抛物线的关系式;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com