
����Ŀ����ͼ����֪���κ���y=ax2+bx+3��a��0����ͼ����A��3��0����B��4��1��������y�ύ�ڵ�C������AB��AC��BC��
��1����˶��κ����Ĺ�ϵʽ��
��2���жϡ�ABC����״������ABC�����Բ��Ϊ��M����ֱ��д��Բ��M�����ꣻ
��3������������������BA����ƽ�ƣ�ƽ�ƺ��A��B��C�Ķ�Ӧ��ֱ��Ϊ��A1��B1��C1 �� ��A1B1C1�����Բ��Ϊ��M1 �� �Ƿ����ij��λ�ã�ʹ��M1����ԭ�㣿�����ڣ������ʱ�����ߵĹ�ϵʽ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�ѵ�A��3��0����B��4��1������y=ax2+bx+3�У�
![]() ��
��
��ã�  ��
��
������������ϵʽΪ��y= ![]() x2��
x2�� ![]() x+3��
x+3��
��2��
�⣺��ABC��ֱ�������Σ�
����B��BD��x���ڵ�D��
��֪��C����Ϊ����0��3��������OA=OC��
���ԡ�OAC=45�㣬
�֡ߵ�B����Ϊ����4��1����
��AD=BD��
���OAC=45�㣬
���BAC=180�㩁45�㩁45��=90�㣬
���ABC��ֱ�������Σ�
Բ��M������Ϊ����2��2����
��3��
�⣺����
ȡBC���е�M������M��ME��y���ڵ�E��
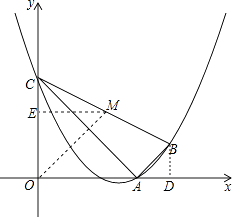
��M����������2��2����
��MC= ![]() =
= ![]() ��OM=2
��OM=2 ![]() ��
��
���MOA=45�㣬
�֡ߡ�BAD=45�㣬
��OM��AB��
��Ҫʹ������������BA����ƽ�ƣ���ʹ��M1����ԭ�㣬
��ƽ�Ƶij���Ϊ��2 ![]() ��
�� ![]() ��2
��2 ![]() +
+ ![]() ��
��
�ߡ�BAD=45�㣬
�������ߵĶ����������¾��ֱ�ƽ�� ![]() =
= ![]() �������
�������
�� ![]() =
= ![]() ����λ���ȣ�
����λ���ȣ�
��y= ![]() x2��
x2�� ![]() x+3=
x+3= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��
��
��ƽ�ƺ������ߵĹ�ϵʽΪ��y= ![]() ��x��
��x�� ![]() +
+ ![]() ��2��
��2�� ![]() ��
�� ![]() ��
��
��y= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��
��
��y= ![]() ��x��
��x�� ![]() +
+ ![]() ��2��
��2�� ![]() ��
�� ![]() ��
��
��y= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��
��
��������������һ��λ�ã�ʹ��M1����ԭ�㣬��ʱ�����ߵĹ�ϵʽΪ��
y= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��y=
��y= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��
��
����������1��ֱ�����ô���ϵ�������a��b��ֵ�����ó��𰸣���2�����ȵó���OAC=45�㣬�����ó�AD=BD�������OAC=45�㣬���ɵó��𰸣���3������������֪�ó�ԲMƽ�Ƶij���Ϊ��2 ![]() ��
�� ![]() ��2
��2 ![]() +
+ ![]() �������ó������ߵ�ƽ�ƹ��ɣ����ɵó��𰸣�
�������ó������ߵ�ƽ�ƹ��ɣ����ɵó��𰸣�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD��EΪƽ��������һ�㣬����DE�����߶�DE�Ƶ�D˳ʱ����ת90��õ�DG������EC��AG��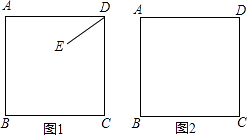
��1������E��������ABCD�ڲ�ʱ��
�������ⲹȫͼ�Σ�
���ж�AG��CE��������ϵ��λ�ù�ϵ��д��֤��˼·��
��2������B��D��G��һ��ֱ��ʱ����AD=4��DG= ![]() ����CE�ij���
����CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����֧��ѩ��ͬʱ��ʼ����ij·�λ�ѩ��һ��ʱ����Ҷӱ���������������3Сʱ�����ʣ�����ѩ������֪��ÿСʱ����ѩ�����ֲ��䣬�Ҷ�ÿСʱ��ѩ50�֣��ס��������ڴ�·�ε���ѩ����y���֣�����ѩʱ��x��ʱ��֮��ĺ���ͼ����ͼ��ʾ�� 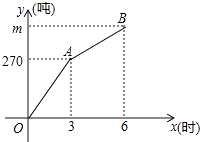
��1���Ҷӵ���ʱ���ס�����������ɵ���ѩ����Ϊ�֣�
��2����˴��������ѩ����m��
��3�����Ҷӵ����y��x֮��ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ÿ��С�����DZ߳�Ϊ1����λ���ȵ�С�����Σ�
��1������ABC����ƽ��3����λ���ȣ�����ƽ�ƺ�ġ�A1B1C1 ��
��2������ABC�Ƶ�O��ת180�㣬������ת��ġ�A2B2C2 ��
��3������һ��ֱ�߽���AC1A2������ֳ���ȵ������֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ʵ���������ࡱ����������Ҫ������Ҫ��A��B��C����ֱ�װ����Ͷ�ţ�����A��ָ�ϵ�أ�����ҩƷ���ж�������B��ָʣ��ʳƷ�ȳ���������C��ָ���ϣ���ֽ�ȿɻ�����������Ͷ����һ����������Ͷ��������������������������ͬ�࣮
��1��ֱ��д����Ͷ�ŵ�����ǡ����A��ĸ��ʣ�
��2������Ͷ�ŵ�����ǡ��һ�����Ͷ�ŵ�������ͬ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬CD�����ߣ�AC=BC��һ���Ե�DΪ�����45����Ƶ�D��ת��ʹ�ǵ����߷ֱ���AC��BC���ӳ����ཻ������ֱ�Ϊ��E��F��DF��AC���ڵ�M��DE��BC���ڵ�N��
��1����ͼ1����CE=CF����֤��DE=DF��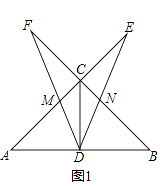
��2����ͼ2���ڡ�EDF�Ƶ�D��ת�Ĺ����У�
��̽�������߶�AB��CE��CF֮���������ϵ����˵�����ɣ�
����CE=4��CF=2����DN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ��ÿ��С�����εı߳���Ϊ1���߶�AB�������˵����С�����εĶ����ϣ�
��1����ͼ�л�����ABΪ�ס����Ϊ12�ĵ�����ABC���ҵ�C��С�����εĶ����ϣ�
��2����ͼ�л���ƽ���ı���ABDE���ҵ�D�͵�E����С�����εĶ����ϣ�tan��EAB= ![]() ������CD����ֱ��д���߶�CD�ij���
������CD����ֱ��д���߶�CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ץס�Ļ������ڵ��̻���ij�̵��������A��B���������ڼ���Ʒ��������A�ּ���Ʒ8����B�ּ���Ʒ3������Ҫ950Ԫ��������A�ּ���Ʒ5����B�ּ���Ʒ6������Ҫ800Ԫ��
��1����A��B���ּ���Ʒÿ���������Ԫ��
��2�������̵�������������ּ���Ʒ��100���������г�������ʽ���ת�����ڹ�����100������Ʒ���ʽ���8 000Ԫ����ô���̵������A�ּ���Ʒ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com