
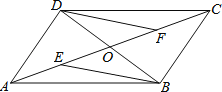
【题目】如图,平行四边形ABCD的对角线AC,BD相交于点O,E、F分别是OA,OC的中点.
(1)求证:BE=DF;
(2)在不添加任何辅助线的情况下写出图中的所有全等三角形.
【答案】(1)见解析;(2)△AOD≌△COB,△AOB≌△COD,△ABC≌△CDA,△ABD≌△CDB,△ABE≌△CDF,△BOE≌△DOF,见解析
【解析】
(1)由平行四边形的性质得出AB=CD,OA=OC,OB=OD,AB∥CD,证出∠BAE=∠DCF,AE=CF,由SAS证明△ABE≌△CDF,即可得出结论;
(2)由平行四边形的性质得出AB=CD,AD=CB,OA=OC,OB=OD,由SAS证明△AOD≌△COB,同理:△AOB≌△COB;由SSS证明△ABC≌△CDA,同理:△ABD≌△CDB;由(1)得:△ABE≌△FD;由SAS证明△BOE≌△DOF即可.
(1)证明:∵四边形ABCD是平行四边形
∴AB=CD,OA=OC,OB=OD,AB∥CD,
∴∠BAE=∠DCF,
∵E、F分别是OA、OC的中点,
∴AE=OE=![]() OA,CF=OF=
OA,CF=OF=![]() OC,
OC,
∴AE=CF,
在△ABE和△CDF中, ,
,
∴△ABE≌△CDF(SAS),
∴BE=DF;
(2)解:图中的所有全等三角形为△AOD≌△COB,△AOB≌△COD,△ABC≌△CDA,△ABD≌△CDB,△ABE≌△CDF,△BOE≌△DOF,理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,AD=CB,OA=OC,OB=OD,
在△AOD和△COB中, ,
,
∴△AOD≌△COB(SAS),
同理:△AOB≌△COB;
在△ABC和△CDA中, ,
,
∴△ABC≌△CDA(SSS),
同理:△ABD≌△CDB;
由(1)得:△ABE≌△FD;
在△BOE和△DOF中, ,
,
∴△BOE≌△DOF(SAS).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形OBDC的对角线相交于点E,其中O(0,0),B(3,4),C(m,0),反比例函数y=![]() (k≠0)的图象经过点B.
(k≠0)的图象经过点B.
(1)求反比例函数的解析式;
(2)若点E恰好落在反比例函数y=![]() 上,求平行四边形OBDC的面积.
上,求平行四边形OBDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一书架上的方格中放置四本厚度和长度相同的书,其中书架方格长BF=40cm,书的长度AB=20cm,设一本书的厚度为xcm.
(1)如图1左边三本书紧贴书架方格内侧竖放,右边一本书自然向左斜放,支撑点为C,E,最右侧书一个角正好靠在方格内侧上,若CG=4cm,求EF的长度;
(2)如图2左边两本书紧贴书架方格内侧竖放,右边两本书自然向左斜放,支撑点为C,E,最右侧书的下面两个角正好靠在方格内上,若∠DCE=30°,求x的值(保留一位小数).(参考数据:![]() =1.414,
=1.414,![]() =1.732)
=1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
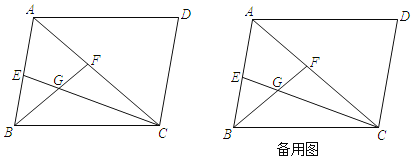
【题目】四边形ABCD为平行四边形,AC为对角线,∠BAC=60°,CE、BF分别∠ACB、∠ABC的角平分线,CE、BF相交于G;
(1)求∠CGF的度数;
(2)求证:BE+CF=BC;
(3)若BE:CF=1:2,EG=2![]() ,求平行四边形ABCD的面积.
,求平行四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“立定跳远”是我市初中毕业生体育测试项目之一.测试时,记录下学生立定跳远的成绩,然后按照评分标准转化为相应的分数,满分10分.其中男生立定跳远的评分标准如下:注:成绩栏里的每个范围,含最低值,不含最高值.
成绩(米) | … | 1.80~1.86 | 1.86~1.94 | 1.94~2.02 | 2.02~2.18 | 2.18~2.34 | 2.34~ |
得分(分) | … | 5 | 6 | 7 | 8 | 9 | 10 |
某校九年级有480名男生参加立定跳远测试,现从中随机抽取10名男生测试成绩(单位:分)如下:
1.96 2.38 2.56 2.04 2.34 2.17 2.60 2.26 1.87 2.32
请完成下列问题:
(1)求这10名男生立定跳远成绩的极差和平均数;
(2)求这10名男生立定跳远得分的中位数和众数;
(3)如果将9分(含9分)以上定为“优秀”,请你估计这480名男生中得优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:

(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售进价分别为120元、190元的![]() 两种型号的电风扇,如下表所示是近二周的销售情况(进价、售价均保持不变,利润
两种型号的电风扇,如下表所示是近二周的销售情况(进价、售价均保持不变,利润![]() 销售收入
销售收入![]() 进货成本):
进货成本):
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 | 5 | 6 | 2310 |
第二周 | 8 | 9 | 3540 |
(1)求![]() 两种型号的电风扇的销售单价;
两种型号的电风扇的销售单价;
(2)若商场再购进这两种型号的电风扇共120台,并且全部销售完,该商场能否实现这两批电风扇的总利润为8240元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com