
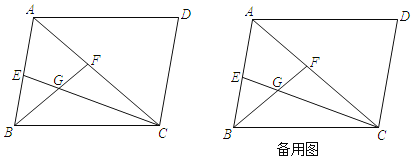
【题目】四边形ABCD为平行四边形,AC为对角线,∠BAC=60°,CE、BF分别∠ACB、∠ABC的角平分线,CE、BF相交于G;
(1)求∠CGF的度数;
(2)求证:BE+CF=BC;
(3)若BE:CF=1:2,EG=2![]() ,求平行四边形ABCD的面积.
,求平行四边形ABCD的面积.
【答案】(1)60°;(2)见解析;(3)180![]()
【解析】
(1)由角平分线的性质和三角形内角和定理可求解;
(2)在BC边上截取CN=CF,连接GN,由“SAS”可证△CGN≌△CG,可得∠CGN=∠CGF=60°,可得∠BGN=∠BGE,由“ASA”可证△BGN≌△BGE,可得BE=BN,可得结论;
(3)设BE=a,CF=2a,AE=c,AF=b,由相似三角形的性质列出方程组,求出 ,通过证明△ABF∽△GEB,可得
,通过证明△ABF∽△GEB,可得![]() ,可求c的值,可得AB,AC,BC的值,即可求平行四边形ABCD的面积.
,可求c的值,可得AB,AC,BC的值,即可求平行四边形ABCD的面积.
解:(1)∵∠BAC=60°,
∴∠ABC+∠ACB=120°,
∵CE、BF分别∠ACB、∠ABC的角平分线,
∴∠GBC+∠GCB=![]() ×120°=60°,
×120°=60°,
∴∠BGC=120°,
∴∠CGF=60°;
故答案为:60°.
(2)在BC边上截取CN=CF,连接GN,如图所示:

在△CGN和△CGF中,
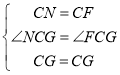 ,
,
∴△CGN≌△CGF(SAS),
∴∠CGN=∠CGF,GF=GN
∵∠BGC=120°,∠CGF=60°,
∴∠BGN=60°,∠EGF=120°,
∴∠BGE=360°﹣120°﹣120°﹣60°=60°,
∴∠BGN=∠BGE,
在△BGN和△BGE中,
 ,
,
∴△BGN≌△BGE(ASA),
∴BE=BN,EG=GN
∴EG=GN=GF
∵BC=BN+CN=BE+CF,
∴BE+CF=BC;
(3)如图,延长CE,DA交于点H,延长BF交AD于点P,过点B作BM⊥AC于M,
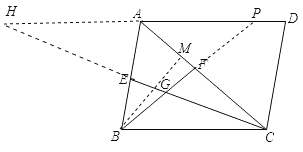
∵BE:CF=1:2,
∴设BE=a,CF=2a,
由(2)可知BC=BE+CF=a+2a=3a,
∵四边形ABCD是平行四边形
∴AD∥BC
∴∠H=∠BCE,∠APB=∠FBC,
∵CE、BF分别∠ACB、∠ABC的角平分线
∴∠ACE=∠BCE,∠ABF=∠CBF
∴∠H=∠ACE,∠APB=∠ABF
∴AH=AC,AP=AB,
设AE=c,AF=b,
∴AB=c+a,AC=b+2a,
∵AH∥BC
∴△AHE∽△BCE
∴![]()
∴![]()
∴b+2a=3c①
∵AH∥BC
∴△APF∽△CBF
∴![]()
∴![]()
∴c+a=![]() b②
b②
由①②组成方程组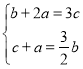
解得:
∴AB=![]() c,AC=3c,
c,AC=3c,
由(2)可知FG=EG=2![]()
∵∠EGB=∠BAC=60°,∠ABF=∠GBE,
∴△ABF∽△GEB,
∴![]()
∴
∴BG=3![]() ,c=8
,c=8
∴a=7,b=10
∴AB=15,AC=24,BC=21,
∵∠BAC=60°,BM⊥AC
∴AM=![]() AB=
AB=![]() ,BM=
,BM=![]() AM=
AM=![]() ,
,
∴SABCD=2S△ABC=2×![]() ×
×![]() ×24=180
×24=180![]()
故答案为:180![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】铜陵市“雨污分流”工程建设期间,某工程队承包了一段总长2400米的地下排水管道铺设任务,按原计划铺设800米后,为尽快完成任务,后来每天的工作效率比原计划提高了25%,结果共用13天完成任务.
(1)求原计划平均每天铺设管道多少米?
(2)若原来每天支付工人工资为2000元,提高工作效率后每天支付给工人的工资增长了30%,则完成整个工程后共支付工人工资多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,AC=BC,∠ACB=90°,直线CP不过点A,B,且不平分∠ACB,点B关于直线CP的对称点为E,直线AE交直线CP于点F.
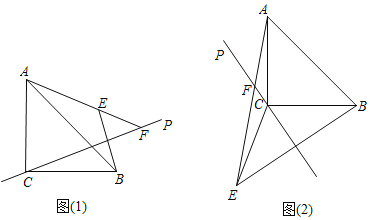
(1)如图1,直线CP与线段AB相交,若∠PCB=25°,求∠CAF的度数;
(2)如图1,当直线CP绕点C旋转时,记∠PCB=α(0°<α<90°,且α≠45°).
①∠FEB的大小是否改变,若不变,求出∠FEB的度数;若改变,请用含α的式子表示).
②找出线段AF,EF,BC的数量关系,并给出证明.
(3)如图2,当直线CP在△ABC外侧,且0°<∠ACP<45°时.若BC=5![]() ,EF=8,求CF的长.
,EF=8,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
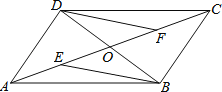
【题目】如图,平行四边形ABCD的对角线AC,BD相交于点O,E、F分别是OA,OC的中点.
(1)求证:BE=DF;
(2)在不添加任何辅助线的情况下写出图中的所有全等三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学要测量学校的国旗杆BD的高度.如图,学校的国旗杆与教学楼之间的距AB=20m.小明在教学楼三层的窗口C测得国旗杆顶点D的仰角为14°,旗杆底部B的俯角为22°.
(1)求∠BCD的大小.
(2)求国旗杆BD的高度(结果精确到1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin14°≈0.24,cos14°≈0.97,tan14°≈0.25)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线: ![]() .
.
(1)求抛物线的顶点坐标.
(2)若直线![]() 经过(2,0)点且与
经过(2,0)点且与![]() 轴垂直,直线
轴垂直,直线![]() 经过抛物线的顶点与坐标原点,且
经过抛物线的顶点与坐标原点,且![]() 与
与![]() 的交点P在抛物线上.求抛物线的表达式.
的交点P在抛物线上.求抛物线的表达式.
(3)已知点A(0,2),点A关于![]() 轴的对称点为点B.抛物线与线段AB恰有一个公共点,结合函数图象写出
轴的对称点为点B.抛物线与线段AB恰有一个公共点,结合函数图象写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校八年级有800名学生,在体育中考前进行一次排球模拟测试,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:

(1)本次抽取到的学生人数为________,图2中![]() 的值为_________.
的值为_________.
(2)本次调查获取的样本数据的平均数是__________,众数是________,中位数是_________.
(3)根据样本数据,估计我校八年级模拟体测中得12分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.

(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com