【题目】已知△ABC中，AB＝13，AC＝15，AD⊥BC于D，且AD＝12，则BC＝ ．
【答案】14或4
【解析】
：（1）如图，锐角△ABC中，AB=13，AC=15，BC边上高AD=12，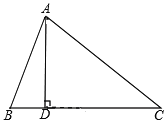
在Rt△ABD中AB=13，AD=12，由勾股定理得
BD2=AB2-AD2=132-122=25，
∴BD=5，
在Rt△ABD中AC=15，AD=12，由勾股定理得
CD2=AC2-AD2=152-122=81，
∴CD=9，
∴BC的长为BD+DC=9+5=14；
（2）钝角△ABC中，AB=13，AC=15，BC边上高AD=12，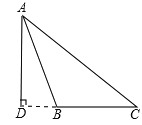
在Rt△ABD中AB=13，AD=12，由勾股定理得
BD2=AB2-AD2=132-122=25，
∴BD=5，
在Rt△ACD中AC=15，AD=12，由勾股定理得
CD2=AC2-AD2=152-122=81，
∴CD=9，
∴BC的长为DC-BD=9-5=4．
故答案为14或4．
金牌课堂练系列答案
三新快车金牌周周练系列答案科目：初中数学 来源： 题型：
【题目】如图，一次函数
的图象与
轴交于点
，与正比例函数
的图象相交于点
，且
．
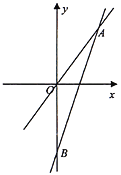
（1）分别求出这两个函数的解析式；
（2）求
的面积；
（3）点
在
轴上，且
是等腰三角形，请直接写出点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，E为AB的中点，FE⊥AB，AF=2AE，FC交BD于O，则∠DOC的度数为（ ）
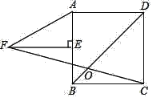
A. 75° B. 54° C. 60° D. 67.5°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知平行四边形OBDC的对角线相交于点E，其中O（0，0），B（3，4），C（m，0），反比例函数y=
（k≠0）的图象经过点B．
（1）求反比例函数的解析式；
（2）若点E恰好落在反比例函数y=上，求平行四边形OBDC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】图1、图2是两张形状，大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，请在图1、图2中分别画出符合要求的图形．（所画图形各顶点必须与方格纸中的小正方形顶点重合）．
（1）在图1中画出一个以线段AB为一边的平行四边形ABCD，使其周长为10+4
．
（2）在图2画出一个周长为20，面积为24的矩形ABCD．
（3）直接写出图1中平行四边形的面积为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
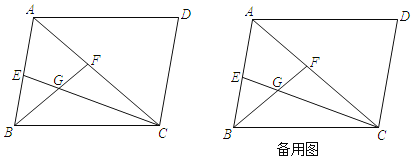
【题目】四边形ABCD为平行四边形，AC为对角线，∠BAC＝60°，CE、BF分别∠ACB、∠ABC的角平分线，CE、BF相交于G；
（1）求∠CGF的度数；
（2）求证：BE+CF＝BC；
（3）若BE：CF＝1：2，EG＝2
，求平行四边形ABCD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
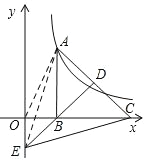
【题目】如图，Rt△ABC 的直角边 BC 在 x 轴的正半轴上，斜边 AC 边中线BD 的反向延长线交 y 轴负半轴于 E，双曲线 y＝
（k＞0）的图象经过点 A， 则△BEC 的面积为____（注：图中参考辅助线已给出）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
