练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

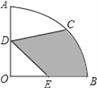
    【题目】如图，在圆心角为90°的扇形OAB中，半径OA=2cm，C为的中点，D、E分别是OA、OB的中点，则图中阴影部分的面积为_____cm2．

    【答案】π+﹣

    【解析】连结OC，过C点作CF⊥OA于F，

    ∵半径OA=2cm，C为的中点，D、E分别是OA、OB的中点，

    ∴OD=OE=1cm，OC=2cm，∠AOC=45°，

    ∴CF=，

    ∴空白图形ACD的面积=扇形OAC的面积﹣三角形OCD的面积

    =﹣

    =π﹣（cm2）

    三角形ODE的面积=OD×OE=（cm2），

    ∴图中阴影部分的面积=扇形OAB的面积﹣空白图形ACD的面积﹣三角形ODE的面积

    =﹣（π﹣）﹣

    =π+﹣（cm2）．

    故图中阴影部分的面积为（π+﹣）cm2．

    故答案为：（π+﹣）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某测量队在山脚A处测得山上树顶仰角为45°（如图），测量队在山坡上前进600米到D处，再测得树顶的仰角为60°，已知这段山坡的坡角为30°，如果树高为15米，则山高为（　　）（精确到1米， =1.732）．

    A. 585米 B. 1014米 C. 805米 D. 820米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC中，AB＝13，AC＝15，AD⊥BC于D，且AD＝12，则BC＝ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明同学要测量学校的国旗杆BD的高度．如图，学校的国旗杆与教学楼之间的距AB=20m．小明在教学楼三层的窗口C测得国旗杆顶点D的仰角为14°，旗杆底部B的俯角为22°．

    （1）求∠BCD的大小．

    （2）求国旗杆BD的高度（结果精确到1m．参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40，sin14°≈0.24，cos14°≈0.97，tan14°≈0.25）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线： .

    （1）求抛物线的顶点坐标．

    （2）若直线经过（2，0）点且与轴垂直，直线经过抛物线的顶点与坐标原点，且与的交点P在抛物线上．求抛物线的表达式．

    （3）已知点A（0，2），点A关于轴的对称点为点B．抛物线与线段AB恰有一个公共点，结合函数图象写出的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

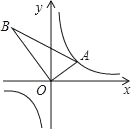
    【题目】如图，△AOB是直角三角形，∠AOB＝90°，OB＝2OA，点A在反比例函数y＝的图象上．若点B在反比例函数y＝的图象上，则k的值为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我校八年级有800名学生，在体育中考前进行一次排球模拟测试，从中随机抽取部分学生，根据其测试成绩制作了下面两个统计图，请根据相关信息，解答下列问题：

    （1）本次抽取到的学生人数为________，图2中的值为_________．

    （2）本次调查获取的样本数据的平均数是__________，众数是________，中位数是_________．

    （3）根据样本数据，估计我校八年级模拟体测中得12分的学生约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为（　　）

    A. 75°B. 60°C. 55°D. 45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

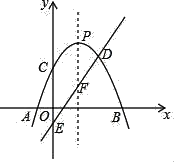
    【题目】如图，抛物线L：y=﹣（x﹣2）2+m2+2m与x轴交于A，B，直线y=kx﹣1与y轴交于E，与L的对称轴交于点F（n，3），与L交于D，抛物线L的对称轴与L交于P．

    (1)求k的值．

    (2)点P能否与点F关于x轴的对称点重合？若认为能，请求出m的值；若认为不能，说明理由．

    (3)小林研究了抛物线L的解析式后，得到了如下的结论：因为m可以取任意实数，所以点C可以在y轴上任意移动，即C点可以到达y轴的任何位置，你认为他说的有道理吗？说说你的想法．

    (4)当抛物线L与直线y=kx﹣1有两个公共点时，直接写出适合条件的m的最大整数．

    查看答案和解析>>

    同步练习册答案