
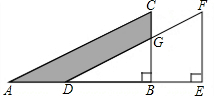
 如图,将直角三角形ABC沿AB方向平移AD的长度得到三角形DEF,已知BE=5,EF=8,CG=4,则图中阴影部分的面积为30.
如图,将直角三角形ABC沿AB方向平移AD的长度得到三角形DEF,已知BE=5,EF=8,CG=4,则图中阴影部分的面积为30. 分析 根据平移的性质可得△DEF≌△ABC,S△DEF=S△ABC,则阴影部分的面积=梯形BEFG的面积,再根据梯形的面积公式即可得到答案.
解答 解:∵ RT△ABC沿AB的方向平移AD距离得△DEF,
RT△ABC沿AB的方向平移AD距离得△DEF,
∴△DEF≌△ABC,
∴EF=BC=8,S△DEF=S△ABC,
∴S△ABC-S△DBG=S△DEF-S△DBG,
∴S四边形ACGD=S梯形BEFG,
∵CG=4,
∴BG=BC-CG=8-4=4,
∴S梯形BEFG=$\frac{1}{2}$(BG+EF)•BE=$\frac{1}{2}$(4+8)×5=30.
故答案为:30.
点评 本题考查了平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.同时考查了梯形的面积公式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限或第二象限 | B. | 第三象限或第四象限 | ||
| C. | 第一象限或第三象限 | D. | 以上答案都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9.5cm | B. | 9.5cm或9cm | C. | 4cm或9.5cm | D. | 9cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com