
【题目】已知![]() 两地相距
两地相距![]() ,甲、乙两人沿同一公路从
,甲、乙两人沿同一公路从![]() 地出发到
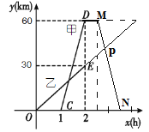
地出发到![]() 地,甲骑摩托车,乙骑自行车,如图中
地,甲骑摩托车,乙骑自行车,如图中![]() 分别表示甲、乙离开
分别表示甲、乙离开![]() 地的距离
地的距离![]() 与时间
与时间![]() 的函数关系的图象,结合图象解答下列问题.
的函数关系的图象,结合图象解答下列问题.
(1)甲比乙晚出发___小时,乙的速度是___![]() ;甲的速度是___
;甲的速度是___![]() .
.
(2)若甲到达![]() 地后,原地休息0.5小时,从
地后,原地休息0.5小时,从![]() 地以原来的速度和路线返回
地以原来的速度和路线返回![]() 地,求甲、乙两人第二次相遇时距离
地,求甲、乙两人第二次相遇时距离![]() 地多少千米?并画出函数关系的图象.
地多少千米?并画出函数关系的图象.

【答案】(1)1,15,60;(2)42,画图见解析.
【解析】
(1)根据函数图象可以解答本题;
(2)根据题意画出函数图像,可以求得![]() 所在直线函数解析式和
所在直线函数解析式和![]() 所在直线的解析式,从而可以解答本题.
所在直线的解析式,从而可以解答本题.
解:(1)由图象可得,甲比乙晚出发1小时,乙的速度是:30÷2=15km/h,甲的速度是:60÷1=60km/h,
故答案为1,15,60;
(2)画图象如图.
设甲在返回时对应的![]() 所在直线函数解析式为:
所在直线函数解析式为:![]() ,
,
由题意可知,M(2.5,60),N(3.5,0),
将点M、N代入可得: ![]() ,解得
,解得![]()
![]() 甲在返回时对应的函数解析式为:
甲在返回时对应的函数解析式为:![]()
设![]() 所在直线的解析式为:
所在直线的解析式为:![]() ,
,
∴![]() ,解得
,解得![]() ,
,
![]() 所在直线的解析式为:
所在直线的解析式为:![]() ,
,
联立![]() ,
,
消去![]() 得
得![]()
答:甲、乙两人第二次相遇时距离![]() 地42千米.
地42千米.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
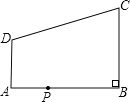
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=![]() ,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(4,0),B(2,0),若点C在一次函数y=![]() x+2的图象上,且△ABC为直角三角形,则满足条件的点C有( )
x+2的图象上,且△ABC为直角三角形,则满足条件的点C有( )
A.4个B.2个C.3个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
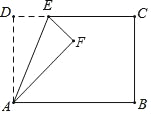
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,AOBC的顶点A、C的坐标分别为A(﹣2,0)、C(0,3),反比例函数的图象经过点B.
(1)求反比例函数的表达式;
(2)这个反比例函数的图象与一个一次函数的图象交于点B、D(m,1),根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)如图,平行四边形OBCD中,OB=8cm,BC=6cm,∠DOB=45°,点P从O沿OB边向点B移动,点Q从点B沿BC边向点C移动,P,Q同时出发,速度都是1cm/s.
(1)求经过O,B,D三点的抛物线的解析式;
(2)判断P,Q移动几秒时,△PBQ为等腰三角形;
(3)若允许P点越过B点在BC上运动,Q点越过C点在CD上运动,设线PQ与OB,BC,DC围成的图形面积为y(cm2),点P,Q的移动时间为t(s),请写出y与t之间的函数关系式,并写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究发现
数学活动课上,小明说“若直线![]() 向左平移3个单位,你能求平移后所得直线所对应函数表达式吗?”
向左平移3个单位,你能求平移后所得直线所对应函数表达式吗?”
经过一番讨论,小组成员展示了他们的解答过程:
在直线![]() 上任取点
上任取点![]() ,
,
向左平移3个单位得到点![]()
设向左平移3个单位后所得直线所对应的函数表达式为![]() .
.
因为![]() 过点
过点![]() ,
,
所以![]() ,
,
所以![]() ,
,
填空:所以平移后所得直线所对应函数表达式为
(2)类比运用
已知直线![]() ,求它关于
,求它关于![]() 轴对称的直线所对应的函数表达式;
轴对称的直线所对应的函数表达式;
(3)拓展运用
将直线![]() 绕原点顺时针旋转90°,请直接写出:旋转后所得直线所对应的函数表达式 .
绕原点顺时针旋转90°,请直接写出:旋转后所得直线所对应的函数表达式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于频率与概率有下列几种说法,其中正确的说法是( )
①“明天下雨的概率是90%”表示明天下雨的可能性很大;
②“抛一枚硬币正面朝上的概率为![]() ”表示每抛两次就有一次正面朝上;
”表示每抛两次就有一次正面朝上;
③“抛一枚硬币正面朝上的概率为![]() ”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在![]() 附近;
附近;
④“某彩票中奖的概率是1%”表示买100张该种彩票不可能中奖.
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人玩摸球游戏:一个不透明的袋子中装有相同大小的3个球,球上分别标有数字1,2,3.首先,甲从中随机摸出一个球,然后,乙从剩下的球中随机摸出一个球,比较球上的数字,较大的获胜.
(1)求甲摸到标有数字3的球的概率;
(2)这个游戏公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com