练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    一元二次方程x2+2x+4=0的根的情况是（　　）

    A．有一个实数根 B．有两个相等的实数根

    C．有两个不相等的实数根 D．没有实数根


    D【考点】根的判别式．

    【分析】判断上述方程的根的情况，只要看根的判别式△=b2﹣4ac的值的符号就可以了．

    【解答】解：∵a=1，b=2，c=4，

    ∴△=b2﹣4ac=22﹣4×1×4=﹣12＜0，

    ∴方程没有实数根．

    故本题选D

    【点评】总结：一元二次方程根的情况与判别式△的关系：

    （1）△＞0⇔方程有两个不相等的实数根；

    （2）△=0⇔方程有两个相等的实数根；

    （3）△＜0⇔方程没有实数根．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C．

    （1）求证:AD平分∠BAC；（2）求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     下列各组数中，能够成直角三角形的是（    ）

     A.  4，5，6          B.  1，1，       C.  6，8，11       D.  5，12，23

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （﹣）2﹣+

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知在代数式a+bx+cx2中，a、b、c都是整数，当x=3时，该式的值是2008；当x=7时，该式的值是2009，这样的代数式有（　　）

    A．0个  B．1个   C．10个 D．无穷多个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


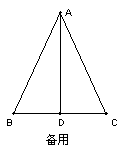
    如图，在△ABC中，AB=AC=13厘米，BC=10厘米,AD⊥BC于点D，动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动,设动点运动时间为秒.

    （1）求AD的长.

    （2）当P、C两点的距离为时，求的值.

    （3）动点M从点C出发以每秒2厘米的速度在射线CB上运动.点M与点P同时出发，且当点P运动到终点D时，点M也停止运动.是否存在，使得S△PMD＝S△ABC？若存在，请求出的值；若不存在，请说明理由.


    查看答案和解析>>

    科目：初中数学 来源： 题型：


               

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列方程是一元二次方程的是（       ）

        A.     B.    C.         D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知的解，则3m+n=__________．

    查看答案和解析>>

    同步练习册答案