
 如图,直线y1=
如图,直线y1=| 1 |
| 2 |
| 5 |
| 2 |
| 9 |
| 2 |
| 5 |
| 1 |
| 2 |
| 5 |
| 2 |
|
|
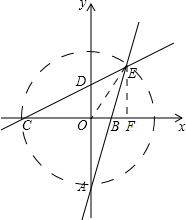 (2)如图,连接OE,过点E作EF⊥x轴于F,以O为圆心,CO的长为半径画圆.
(2)如图,连接OE,过点E作EF⊥x轴于F,以O为圆心,CO的长为半径画圆.| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
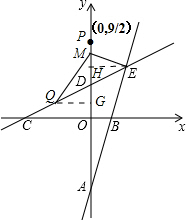 (3)如图,过点Q作QG⊥y轴于G,过点E作EH⊥y轴于H,
(3)如图,过点Q作QG⊥y轴于G,过点E作EH⊥y轴于H,| 5 |
| 2 |
5
| ||
| 2 |
| QD |
| DC |
| QG |
| CO |
| 5 |
| 9 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| t |
| 2 |
| ||
| 2•(-1) |
| 1 |
| 4 |


科目:初中数学 来源: 题型:
 如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1,S2,S3分别表示这三个正方形的面积,S1=81,S2=225,则S3=( )
如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1,S2,S3分别表示这三个正方形的面积,S1=81,S2=225,则S3=( )| A、16 | B、306 |
| C、144 | D、12 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,利用一面长为34米的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏)设矩形ABCD的边AD长为x米,AB长为y米,矩形的面积为S平方米,且x<y.
如图,利用一面长为34米的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏)设矩形ABCD的边AD长为x米,AB长为y米,矩形的面积为S平方米,且x<y.查看答案和解析>>
科目:初中数学 来源: 题型:
 如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么,我们称抛物线C1与C2关联.
如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么,我们称抛物线C1与C2关联.| 1 |
| 8 |
| 1 |
| 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
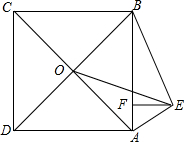 如图,以正方形ABCD的一边AB为斜边向外作Rt△AEB,过点E作EF⊥AB,连接EO
如图,以正方形ABCD的一边AB为斜边向外作Rt△AEB,过点E作EF⊥AB,连接EO查看答案和解析>>
科目:初中数学 来源: 题型:
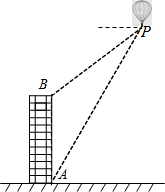 如图,利用热气球探测器测量大楼AB的高度.从热气球P处测得大楼顶部B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离地面的高度为120m.试求大楼AB的高度(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
如图,利用热气球探测器测量大楼AB的高度.从热气球P处测得大楼顶部B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离地面的高度为120m.试求大楼AB的高度(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com