
【题目】如图:△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
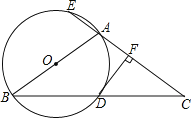
(1)试说明DF是⊙O的切线;
(2)若AC=3AE,求DF:CF.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,求出OD∥AC,求出DF⊥OD,根据切线的判定得出即可;
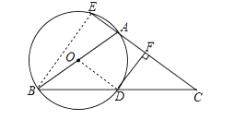
(2)连结BE,由AB是直径可知∠AEB=90°,由AC=3AE可得AB=AC=3AE,EC=4AE,再证明△CFD∽△CEB,得到![]() ,即可求出.
,即可求出.
(1)连接OD,
∵OB=OD,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,点D在⊙O上,
∴DF是⊙O的切线;
(2)连接BE,
∵AB是直径,
∴∠AEB=90°,
∵AB=AC,AC=3AE,
∴AB=3AE,CE=4AE,
BE=![]() ,
,
∵DF⊥CE,
∴DF∥BE,
∴△CFD∽△CEB,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】某种商品每天的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间满足关系:
(元)之间满足关系:![]() ,其图像如图所示.
,其图像如图所示.
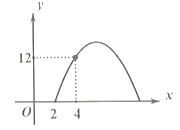
(1)销售单价为多少元时,这种商品每天的销售利润最大?最大利润为多少元?
(2)若该商品每天的销售利润不低于12元,则销售单价![]() 的取值范围是_____.
的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,每件的成本每千克18元,规定每千克售价不低于成本,且获利不得高于100%,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 40 | 39 | 38 | 37 |
销售量y(千克) | 20 | 22 | 24 | 26 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
(3)该超市若想每天销售利润不低于480元,请结合函数图象帮助超市确定产品的销售单价范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的顶点A,B,C的坐标分别是A(﹣1,﹣1),B(﹣4,﹣1),C(﹣4,﹣3).
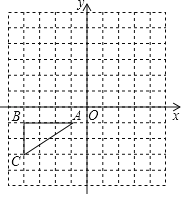
(1)作出△ABC关于原点O中心对称的图形△A1B1C1,并写出点B的对应点B1的坐标;
(2)作出△A1B1C1绕原点O顺时针旋转90°后的图形△A2B2C2,并写出点C1的对应点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,
(1)求证:△EBC是等腰三角形;
(2)已知:AB=7,BC=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节放假期间,小明和小华准备到宜宾的蜀南竹海(记为A)、兴文石海(记为B)、夕佳山民居(记为C)、李庄古镇(记为D)的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点都被选中的可能性相同.
(1)小明选择去蜀南竹海旅游的概率为 .
(2)用树状图或列表的方法求小明和小华都选择去兴文石海旅游的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的![]() .
.
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
⑴请你补全这个输水管道的圆形截面;
⑵若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
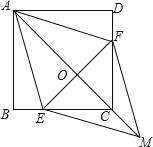
【题目】如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:CE=CF.
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com