
����Ŀ��ij��������һ����Ʒ��ÿ���ijɱ�ÿǧ��18Ԫ���涨ÿǧ���ۼ۲����ڳɱ����һ������ø���100%�����г����飬ÿ���������y(ǧ��)��ÿǧ���ۼ�x(Ԫ)����һ�κ�����ϵ�������������±���
�ۼ�x(Ԫ/ǧ��) | 40 | 39 | 38 | 37 |
������y(ǧ��) | 20 | 22 | 24 | 26 |
(1)��y��x֮��ĺ�������ʽ��
(2)����Ʒÿ���������ΪW(Ԫ)����W��x֮��ĺ�������ʽ(�������멁�ɱ�)����ָ���ۼ�Ϊ����Ԫʱ������������������Ƕ��٣�
(3)�ó�������ÿ������������480Ԫ�����Ϻ���ͼ���������ȷ����Ʒ�����۵��۷�Χ��
���𰸡�(1)y����2x+100�� (2���ۼ�Ϊ34Ԫʱ�������������������512��(3)���ڼ��̳�ÿ�첻����480Ԫ�����۵��۲�����30Ԫ������36Ԫ��
��������
��1����y��x�ĺ�����ϵʽΪy=kx+b����x=40��y=20��x=37��y=26�ֱ�������k��b��
��2����������=���ۼ�-�ɱ������������г�������ϵʽ��
��3���ⷽ�̵õ�x��Ȼ��������ۣ�
(1)��y��x�ĺ�����ϵʽΪy��kx+b����x��40��y��20��x��37��y��26�ֱ�����![]()
���![]()
��y��x֮��ĺ�������ʽΪ��y����2x+100��
(2)��W��(x��18)y��
��y����2x+100����ã�W��(x��18)(��2x+100)��
��W����2x2+136x��1800����2(x��34)2+512��
�൱�ۼ�Ϊ34Ԫʱ�������������������512��
(3)��������é�2x2+136x��1800��480��
��ã�x1��38��x2��30��
�������ڼ䵥�۲����ڳɱ����ۣ������ֲ��ø���100%��
��18��x��36
x2��38�������⣬Ӧ��ȥ��
����30��x��36��W��480��
�����ڼ��̳�ÿ�첻����480Ԫ�����۵��۲�����30Ԫ������36Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E��������ABCD�ı�DC��һ�㣬�ѡ�ADE˳ʱ����ת��ABF��λ�ã�
��1����ת�����ǵ� ����ת�Ƕ����������������ȣ�
��2��������EF�����AEF�� �����Σ���֤����
��3�����ı���AECF�����Ϊ25��DE=2����AE�ij���
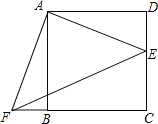
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y1=��x+4��y2=![]() x+b����˫����y=
x+b����˫����y=![]() ���ڵ�A��1��m����������ֱ�߷ֱ���x�ύ��B��C���㣮
���ڵ�A��1��m����������ֱ�߷ֱ���x�ύ��B��C���㣮
��1����y��x֮��ĺ�����ϵʽ��
��2��ֱ��д����x��0ʱ������ʽ![]() x+b��
x+b��![]() �Ľ⼯��
�Ľ⼯��
��3������P��x���ϣ�����AP����ABC������ֳ�1��3�����֣����ʱ��P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �Ǻ���
�Ǻ���![]() �����㣬
�����㣬![]() Ϊһ���㣬��
Ϊһ���㣬��![]() �ᣬ
�ᣬ![]() �ᣬ����˵����ȷ����( )
�ᣬ����˵����ȷ����( )

��![]() ����
����![]() ������
������![]() ����
����![]() ƽ��
ƽ��![]() ������
������![]() ����
����![]()
A. �٢� B. �ڢ� C. �ڢ� D. �ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�麬30��ǵ�ֱ�����ǰ�OAB��ֱ�DZ�BO�ij�ǡ����һ�����ֱ�����ǰ�ODC��б��OC�ij���ȣ������������ǰ������ƽ��ֱ������ϵ�У���OB��3![]() .
.
(1)��ij������������ͼ���һ����֧ǡ�þ�����A������������������Ľ���ʽ��
(2)���Ѻ�30��ǵ�ֱ�����ǰ��Ƶ�O��˳ʱ�뷽����ת��б��OAǡ������x���ϣ���A���ڵ�A�䴦������ͼ����Ӱ���ֵ������(���������)
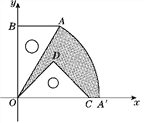
���𰸡�(1)�����������Ľ���ʽΪy��![]() ��(2)S��Ӱ��6�У�
��(2)S��Ӱ��6�У�![]() .
.
����������������1������tan30��=![]() �����AB���������OA���ó�A�����꣬���A��˫���ߵĽ���ʽ��y=
�����AB���������OA���ó�A�����꣬���A��˫���ߵĽ���ʽ��y=![]() ����A���������������ɣ���2�������AOA�䣬�������ε������ʽ�������AOA�����������OD��DC���������ODC������������������𰸣�
����A���������������ɣ���2�������AOA�䣬�������ε������ʽ�������AOA�����������OD��DC���������ODC������������������𰸣�
���������
(1)��Rt��OBA�У���AOB��30�㣬OB��3![]() ��
��
��AB��OB��tan 30�㣽3.
���A������Ϊ(3��3![]() )��
)��
�跴���������Ľ���ʽΪy��![]() (k��0)��
(k��0)��
��3![]() ��
��![]() ����k��9
����k��9![]() ������������������Ľ���ʽΪy��
������������������Ľ���ʽΪy��![]() .
.
(2)��Rt��OBA�У���AOB��30�㣬AB��3��
sin ��AOB��![]() ����sin 30�㣽
����sin 30�㣽![]() ��
��
��OA��6.
������ã���AOC��60�㣬S����AOA����![]() ��6��.
��6��.
��Rt��OCD�У���DOC��45�㣬OC��OB��3![]() ��
��
��OD��OC��cos 45�㣽3![]() ��
��![]() ��
��![]() .
.
��S��ODC��![]() OD2��
OD2��![]()
![]() ��
��![]() .
.
��S��Ӱ��S����AOA����S��ODC��6����![]() .
.
�㾦�����⿼���˹��ɶ���������ϵ������������ʽ������ǵ����Ǻ���ֵ�����ε���������������ε����ʣ����������е��⣬�ѶȲ����������ͼ�ε������ʾ�ɶ������ͼ�ε����֮���ǽ����Ĺؼ�.
�����͡������
��������
26
����Ŀ������ABCDһ����AD��8��������ABCD�۵���ʹ�õ�B����CD���ϵĵ�P����
(1)��ͼ�٣���֪�ۺ����BC���ڵ�O������AP��OP��OA.
�� ��֤����OCP�ס�PDA��
�� ����OCP���PDA�������Ϊ1:4�����AB�ij���
(2)��ͼ�ڣ���(1)�������£���ȥAO��OP������BP.����M���߶�AP��(�����P��A�غ�)������N���߶�AB���ӳ����ϣ���BN��PM������MN��PB�ڵ�F����ME��BP�ڵ�E.���ʶ���M��N���ƶ��Ĺ����У��߶�EF�ij����Ƿ����仯�������䣬����߶�EF�ij��ȣ����仯��˵�����ɣ�
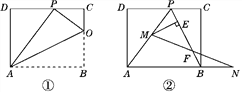
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ѧ����Ϊ���㾭֮�ס��ġ��������������й��Ŵ��㷨�Ŀ���֮��.�������������м��أ���������ȸ�����࣬����֮�⣬ȸ���أ������.һȸһ�ཻ����������ƽ.���ࡢȸ��һ��.���ࡢȸһö���ؼ��Σ���
���ģ�������5ֻȸ��6ֻ�࣬�ֱ�ۼ������ú�����֮������һ���ȸ�أ�����.��һֻȸ��һֻ�ཻ��λ�ö��ţ��������.5ֻȸ��6ֻ������Ϊ1��.��ȸ������ֻ���ض��ٽ��
��ÿֻȸ��x�ÿֻ����y����з�����Ϊ_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ����D��BC������һ�㣬���߶�AD�Ƶ�A��ʱ�뷽����ת
����D��BC������һ�㣬���߶�AD�Ƶ�A��ʱ�뷽����ת![]() ���õ��߶�AE������EC��
���õ��߶�AE������EC��
![]() �����ⲹȫͼ�Σ�
�����ⲹȫͼ�Σ�
![]() ��
��![]() �Ķ�����
�Ķ�����
![]() ��
��![]() ��
��![]() ��������DA�Ƶ�D˳ʱ����ת
��������DA�Ƶ�D˳ʱ����ת![]() ��EC���ӳ����ڵ�F����д����AF����˼·��
��EC���ӳ����ڵ�F����д����AF����˼·��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڷ���������y��![]() ��k��0���������������ĸ������У���ȷ���ǣ�������
��k��0���������������ĸ������У���ȷ���ǣ�������
A. ���㣨2��4������ͼ���ϣ���2��4��Ҳ����ͼ����
B. ��k��0ʱ��y��x���������С
C. ��ͼ������һ��P��x�ᡢy��Ĵ��ߣ�����ֱ�A��B�������OAPB�����Ϊk
D. ������������ͼ�����ֱ��y��x��y����x����Գ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�ABC�У���ACB��90�㣬BC��2����A��30�㣬��E��F�ֱ����߶�BC��AC���е㣬����EF��
��1���߶�BE��AF��λ�ù�ϵ���� ����![]() ���� ����
���� ����
��2����ͼ2������CEF�Ƶ�C˳ʱ����תaʱ��0�㣼a��180�㣩������AF��BE����1���еĽ����Ƿ���Ȼ�����������������֤�����������������˵�����ɣ�
��3����ͼ3������CEF�Ƶ�C˳ʱ����תaʱ��0�㣼a��180�㣩���ӳ�FC��AB�ڵ�D�����AD��6��2![]() ������ת��a�Ķ�����
������ת��a�Ķ�����
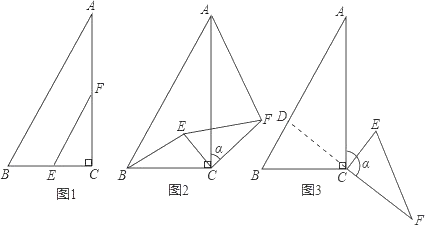
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com