
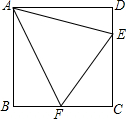
 正方形ABCD中,∠EAF=45°.求证:EF=BF+DE.
正方形ABCD中,∠EAF=45°.求证:EF=BF+DE. 分析 先由正方形的性质得AB=AD,∠BAC=∠D=∠ABC=90°,则可把△AED绕点A顺时针旋转90°得到△ABG,如图,根据旋转的性质得AG=AE,BG=DE,∠EAG=90°,∠ABG=∠D=90°,于是可判断点G在CB的延长线上,得到BF+BG=GF,然后证明△AEF≌△AGF得到EF=FG,于是有EF=BF+BG=BF+DE.
解答 证明:∵四边形ABCD为正方形,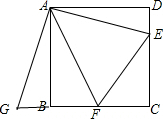
∴AB=AD,∠BAC=∠D=∠ABC=90°,
∴把△AED绕点A顺时针旋转90°得到△ABG,如图,
∴AG=AE,BG=DE,∠EAG=90°,∠ABG=∠D=90°,
∴点G在CB的延长线上,
∴BF+BG=GF,
∵∠EAF=45°,
∴∠GAF=45°,
在△AEF和△AGF中,
$\left\{\begin{array}{l}{AF=AF}\\{∠EAF=∠GAF}\\{AE=AG}\end{array}\right.$,
∴△AEF≌△AGF,
∴EF=FG,
∴EF=BF+BG=BF+DE.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质和三角形全等的判定与性质.


科目:初中数学 来源: 题型:填空题
 北京紫禁城是中国古代汉族宫廷建筑之精华.经测算发现,太和殿,中和殿,保和殿这三大殿的矩形宫院ABCD(北至保和殿,南至太和门,西至弘义阁,东至体仁阁)与三大殿下的工字形大台基所在的矩形区域EFGH为相似形.若比较宫院与台基之间的比例关系,可以发现接近于9:5,取“九五至尊”之意.根据测量数据,三大殿台基的宽为40丈,请你估算三大殿宫院的宽为72丈.
北京紫禁城是中国古代汉族宫廷建筑之精华.经测算发现,太和殿,中和殿,保和殿这三大殿的矩形宫院ABCD(北至保和殿,南至太和门,西至弘义阁,东至体仁阁)与三大殿下的工字形大台基所在的矩形区域EFGH为相似形.若比较宫院与台基之间的比例关系,可以发现接近于9:5,取“九五至尊”之意.根据测量数据,三大殿台基的宽为40丈,请你估算三大殿宫院的宽为72丈.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
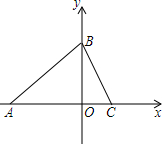 如图,在平面直角坐标系中,点C在x轴正半轴上,点B在y轴正半轴上,且AB=AC.点B到x轴的距离为3.
如图,在平面直角坐标系中,点C在x轴正半轴上,点B在y轴正半轴上,且AB=AC.点B到x轴的距离为3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
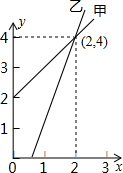 如图是甲、乙两家商店销售A种商品的销售价y(元)与销售量x(件)之间的函数的图象,请根据图象提供的信息,写出4个你认为正确的结论:
如图是甲、乙两家商店销售A种商品的销售价y(元)与销售量x(件)之间的函数的图象,请根据图象提供的信息,写出4个你认为正确的结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
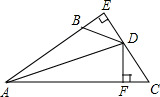 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AB+AC=2AE中正确的是①②④.
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AB+AC=2AE中正确的是①②④.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com