
【题目】如图,在等边△ABC中,点D、E分别在BC、AC上,且BD=CE,连接AD,BE交于点F;
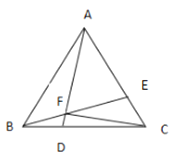
(1)求∠AFE的度数;
(2)连接FC,若∠AFC=90°,BF=1,求AF的长.
【答案】(1)60°;(2)2.
【解析】
(1)因为△ABC为等边三角形,所以∠ABD=∠BCE=60°,AB=AC=BC,又BD=CE,所以用“SAS”可判定△ABD≌△BCE,根据全等三角形的性质得出∠BAD=∠CBE,利用三角形外角性质解答即可;
(2)延长BE至H,使FH=AF,连接AH,CH,得到:△ACH,利用等边三角形的性质进而解答即可.
解:(1)∵△ABC为等边三角形,
∴AB=AC=BC,∠ABD=∠BCE=60°,
在△ABD和△BCE中,
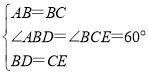 ,
,
∴△ABD≌△BCE(SAS);
∴∠BAD=∠CBE,
∵∠ADC=∠CBE+∠BFD=∠BAD+∠B,
∴∠BFD=∠B=∠AFE=60°;
(2)
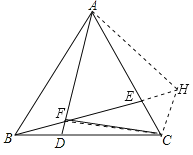
延长BE至H,使FH=AF,连接AH,CH
由(1)知∠AFE=60°,∠BAD=∠CBE,
∴△AFH是等边三角形,
∴∠FAH=60°,AF=AH,
∴∠BAC=∠FAH=60°,
∴∠BAC-∠CAD=∠FAH-∠CAD,
即∠BAF=∠CAH,
在△BAF和△CAH中,
∵AB=AC,∠BAF=∠CAH,AF=AH,
∴△BAF≌△CAH(SAS),
∴∠ABF=∠ACH,CH=BF=1;
又∵∠ABC=∠BAC,∠BAD=∠CBE,
∴∠ABC-∠CBE=∠BAC-∠BAD,
即∠ABF=∠CAF,
∴∠ACH=∠CAF,
∴AF∥CH,
∵∠AFC=90°,∠AFE=60°,
∴CF⊥CH,∠CFH=30°,
∴FH=2CH,
∴AF=2BF=2×1=2,
即AF的长为2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】红星中学九年级(1)班三位教师决定带领本班![]() 名学生利用假期去某地旅游,枫江旅行社的收费标准为:教师全价,学生半价;而东方旅行社不管教师还是学生一律八折优惠,这两家旅行社的全价都是500元。
名学生利用假期去某地旅游,枫江旅行社的收费标准为:教师全价,学生半价;而东方旅行社不管教师还是学生一律八折优惠,这两家旅行社的全价都是500元。
(1)用含![]() 的式子表示三位教师和
的式子表示三位教师和![]() 位学生参加这两家旅行社所需的费用各是多少元;
位学生参加这两家旅行社所需的费用各是多少元;
(2)如果![]() =50时,请你计算选择哪一家旅行社较为合算?
=50时,请你计算选择哪一家旅行社较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入_____元.
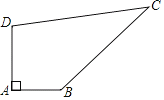
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出无鱼水缸内最高水位![]() 与注水时间
与注水时间![]() 之间的变化情况的是( )
之间的变化情况的是( )
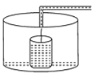
A. B.
B.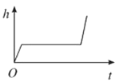
C.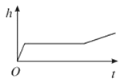 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,A点坐标为(-10,0),对角线AC和OB相交于点D且AC·OB=160.若反比例函数y=![]() (x<0)的图象经过点D,并与BC的延长线交于点E,则S△OCE∶S△OAB=________.
(x<0)的图象经过点D,并与BC的延长线交于点E,则S△OCE∶S△OAB=________.
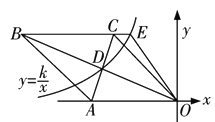
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.
,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.
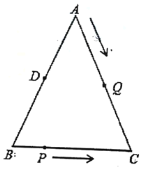
(1)若点P、Q两点分别从B、A两点同时出发,经过2秒后,![]() 与
与![]() 是否全等?请说明理由;
是否全等?请说明理由;
(2)若点P、Q两点分别从B、A两点同时出发,![]() 的周长为16cm,设运动时间为t,问:当t为何值时,是等腰三角形?
的周长为16cm,设运动时间为t,问:当t为何值时,是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O(0,0),B(1,2).
(1)若点A在y轴上,且三角形AOB的面积为2,求点A的坐标;
(2)若点C的坐标为(3,0),BD∥OC,且BD=OC,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等角转化;如图1,已知点A是BC外一点,连结AB、AC,求∠BAC+∠B+∠C的度数.
(1)阅读并补充下面的推理过程
解:过点A作ED∥BC,
∴∠B=∠EAB,∠C= ( )
又∵∠EAB+∠BAC+∠DAC=180°
∴∠B+∠BAC+∠C=180°
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC、∠B、∠C“凑”在一起,得出角之间的关系,使问题得以解决.
(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数(提示:过点C作CF∥AB);
(3)如图3,已知AB∥CD,点C在点D的右侧,∠ADC=80°,点B在点A的左侧,∠ABC=60°,BE平分∠ABC,DE平分∠ADC,BE、DE所在的直线交于点E,点E在两条平行线AB与CD之间,求∠BED的度数.
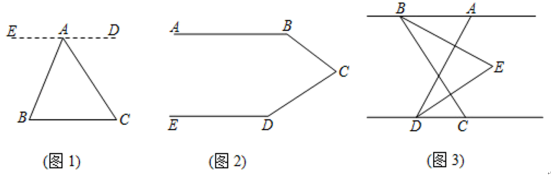
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解决有关问题
我们知道:
|a|=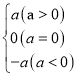
现在我们可以用这一结论来化解含有绝对值的代数式
如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1和x=2(称﹣1,2分别为|x+1|和|x﹣2|的零点值)
在实数范围内,零点值x=﹣1和x=2可将全体实数分成不重复且不遗漏的如下三种情况:
(1)x<﹣1(2)﹣1≤x<2(3)x≥2
从而化简代数式|x+1|+|x﹣2|,可分以下三种情况
(1)x<﹣1时,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1
(2)﹣1≤x<2时,原式=x+1﹣(x﹣2)=3
(3)x≥2时,原式=x+1+x﹣2=2x﹣1
通过以上阅读,请你解决以下问题
(1)化简代数式|x+2|+|x﹣4|
(2)求|x﹣1|﹣4|x+1|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com