
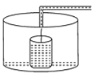
【题目】小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出无鱼水缸内最高水位![]() 与注水时间
与注水时间![]() 之间的变化情况的是( )
之间的变化情况的是( )
A. B.
B.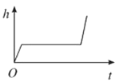
C.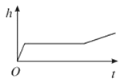 D.
D.
【答案】C
【解析】
依题意无水鱼缸内最高水位![]() 与注水时间
与注水时间![]() 之间的情况有三段变化情况,第一段过程是水入玻璃杯,第二段过程是水满玻璃杯进入无水鱼缸内,第三段过程是进入无水鱼缸内的水位超过玻璃杯最高水位
之间的情况有三段变化情况,第一段过程是水入玻璃杯,第二段过程是水满玻璃杯进入无水鱼缸内,第三段过程是进入无水鱼缸内的水位超过玻璃杯最高水位![]()
依题意无水鱼缸内最高水位![]() 与注水时间
与注水时间![]() 之间的情况有三段变化情况,第一段过程是水入玻璃杯最高水位
之间的情况有三段变化情况,第一段过程是水入玻璃杯最高水位![]() 变化较快,第二段过程是水满玻璃杯进入无水鱼缸内最高水位
变化较快,第二段过程是水满玻璃杯进入无水鱼缸内最高水位![]() 维持一段时间不变,第三段过程是进入无水鱼缸内的水位超过玻璃杯最高水位
维持一段时间不变,第三段过程是进入无水鱼缸内的水位超过玻璃杯最高水位![]() ,最高水位
,最高水位![]() 增加缓慢.
增加缓慢.
A水位随时间变化一直保持不变,不对.
B水位随时间变化第一段较快,第二段维持一段时间不变,第三段比第一段变化还快,不对
C符合水位随时间变化第一段较快,第二段维持一段时间不变,第三段缓慢变化,正确
D第二段没有维持一段时间不变
本题答案是:C


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
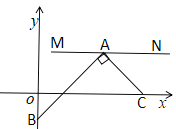
【题目】如图,在平面直角坐标系中,M、N、C三点的坐标分别为(![]() ,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作
,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作![]() 交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
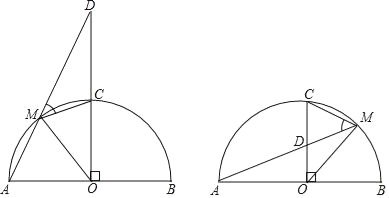
【题目】如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是![]() 上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
(1)若半圆的半径为10.
①当∠AOM=60°时,求DM的长;
②当AM=12时,求DM的长.
(2)探究:在点M运动的过程中,∠DMC的大小是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:
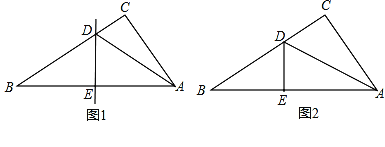
操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,可求得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为 ;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产记为正、减产记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
增减产值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知该厂星期五生产自行车__________辆.
(2)根据记录的数据可知该厂本周实际生产自行车_________辆.
(3)该厂实行每日计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元,若没有完成任务,少生产一辆扣20元,那么该厂工人这一周的工作总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20m有一棵树C,继续前行20m到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米.
(1)河的宽度是 米.
(2)请你说明他们做法的正确性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D、E分别在BC、AC上,且BD=CE,连接AD,BE交于点F;
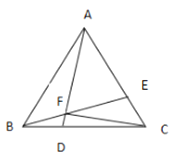
(1)求∠AFE的度数;
(2)连接FC,若∠AFC=90°,BF=1,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家家乐超市购进一批面粉,标准质量为50千克,现抽取20袋面粉进行称重检测,为记录的方便用![]() ,表示超过标准的重量,用
,表示超过标准的重量,用![]() 表示不足标准的重量,结果如下表(单位:千克)
表示不足标准的重量,结果如下表(单位:千克)
与标准差(千克) | -2 | -1.5 | -1 | -0.5 | 0 | 0.5 | 1 | 1.5 |
袋数 | 3 | 2 | 3 | 4 | 1 | 2 | 1 | 4 |
(1)求这20袋面粉超出或不足的质量为多少?
(2)这20袋面粉平均每袋多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.

(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2![]() ,求正方形ADCE周长.
,求正方形ADCE周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com