
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:
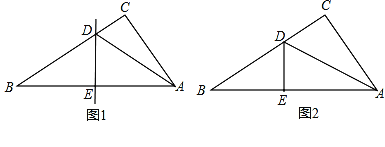
操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,可求得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为 ;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
【答案】操作一(1) 14cm (2) 35° 操作二 CD=4.5
【解析】
试题:操作一利用对称找准相等的量:BD=AD,∠BAD=∠B,然后分别利用周长及三角形的内角和可求得答案;
操作二 利用折叠找着AC=AE,利用勾股定理列式求出AB,设CD=x,表示出BD,AE,在Rt△BDE中,利用勾股定理可得答案;
试题解析:操作一:
(1)由折叠的性质可得AD=BD,∵△ACD的周长=AC+CD+AD,
∴△ACD的周长=AC+CD+BD=AC+BC=8+6=14(cm);
(2)设∠CAD=4x,∠BAD=7x由题意得方程:
7x+7x+4x=90,
解之得x=5,
所以∠B=35°;
操作二:∵AC=9cm,BC=12cm,
∴AB=![]() (cm),
(cm),
根据折叠性质可得AC=AE=9cm,
∴BE=AB-AE=6cm,
设CD=x,则BD=12-x,DE=x,
在Rt△BDE中,由题意可得方程x2+62=(12-x)2,
解之得x=4.5,
∴CD=4.5cm.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与y轴交于A点,与反比例函数y= ![]() (x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).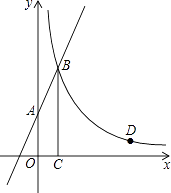
(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y= ![]() (x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点 ![]() ,点
,点 ![]() .对
.对 ![]() 点作下列变换:①先 把点
点作下列变换:①先 把点 ![]() 向右平移
向右平移 ![]() 个单位,再向上平移
个单位,再向上平移 ![]() 个单位;②先把点
个单位;②先把点 ![]() 向上平移
向上平移 ![]() 个单位,再向右平移
个单位,再向右平移 ![]() 个单位;③先作点
个单位;③先作点 ![]() 以
以 ![]() 轴为对称轴的轴对称变换,再向左平移
轴为对称轴的轴对称变换,再向左平移 ![]() 个单位;④先作点
个单位;④先作点 ![]() 以
以 ![]() 轴为对称轴的轴对称变换,再向右平移
轴为对称轴的轴对称变换,再向右平移 ![]() 个单位,其中能由点
个单位,其中能由点 ![]() 得到点
得到点 ![]() 的变换 是_________。
的变换 是_________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα= ![]() ,则线段CE的最大值为 .
,则线段CE的最大值为 . 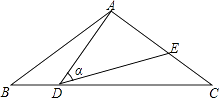
查看答案和解析>>
科目:初中数学 来源: 题型:
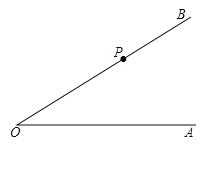
【题目】按照下列要求画图并填空:
如图,点![]() 是
是![]() 的边
的边![]() 上的一点,
上的一点,
(1)过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ;
;
(2)在(1)的基础上作![]() 的边
的边![]() 上的高,垂足为
上的高,垂足为![]() ;
;
(3)线段___________的长度是点![]() 到直线
到直线![]() 的距离;
的距离;
(4)线段![]() 这三条线段大小关系是___________(用“<”号连接).
这三条线段大小关系是___________(用“<”号连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由一些棱长都为1的小正方体组合成的简单几何体.

![]() 该几何体的表面积
该几何体的表面积![]() 含下底面
含下底面![]() 为______;
为______;
![]() 请画出这个几何体的三视图并用阴影表示出来;
请画出这个几何体的三视图并用阴影表示出来;
![]() 如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加______个小正方体.
如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加______个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为37°,塔底B的仰角为26.6°.已知塔高BC=80米,塔所在的山高OB=220米,OA=200米,图中的点O、B、C、A、P在同一平面内,求山坡的坡度.(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin37°≈0.60,tan37°≈0.75)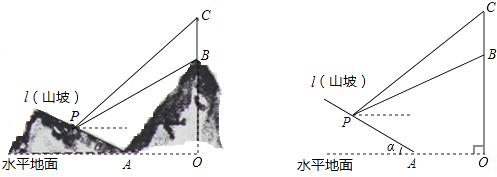
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com