
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC=![]() ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是__.
,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是__.
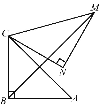
【答案】﹢1
【解析】
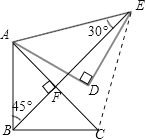
试题首先考虑到BE所在的三角形并不是特殊三角形,所以猜想到要求BE,可能需要构造直角三角形.由旋转的性质可知,AC=AE,∠CAE=60°,故△ACE是等边三角形,可证明△ABE与△CBE全等,可得到∠ABE=45°,∠AEB=30°,再证△AFB和△AFE是直角三角形,然后在根据勾股定理求解
解:连结CE,设BE与AC相交于点F,如下图所示,
∵Rt△ABC中,AB=BC,∠ABC=90°
∴∠BCA=∠BAC=45°
∵Rt△ABC绕点A逆时针旋转60°与Rt△ADE重合,
∴∠BAC=∠DAE=45°,AC=AE
又∵旋转角为60°
∴∠BAD=∠CAE=60°,
∴△ACE是等边三角形
∴AC=CE=AE=4
在△ABE与△CBE中,![]()
∴△ABE≌△CBE (SSS)
∴∠ABE=∠CBE=45°,∠CEB=∠AEB=30°
∴在△ABF中,∠BFA=180°﹣45°﹣45°=90°
∴∠AFB=∠AFE=90°
在Rt△ABF中,由勾股定理得,
BF=AF=![]() =2
=2
又在Rt△AFE中,∠AEF=30,°∠AFE=90°
FE=AF=2
∴BE=BF+FE=2+2
故,本题的答案是:2+2


科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作![]() 中
中![]() 边上的高线”的尺规作图过程.
边上的高线”的尺规作图过程.
已知:![]() .
.
求作:![]() 中
中![]() 边上的高线
边上的高线![]() .
.
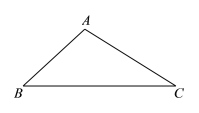
作法:如图,
①以点![]() 为圆心,
为圆心,![]() 的长为半径作弧,以点
的长为半径作弧,以点![]() 为圆心,
为圆心,![]() 的长为半径作弧,两弧在
的长为半径作弧,两弧在![]() 下方交于点
下方交于点![]() ;
;
②连接![]() 交
交![]() 于点
于点![]() .
.
所以线段![]() 是
是![]() 中
中![]() 边上的高线.
边上的高线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵ ![]() ,
, ![]() ,
,
∴点![]() ,
,![]() 分别在线段
分别在线段![]() 的垂直平分线上( )(填推理的依据).
的垂直平分线上( )(填推理的依据).
∴![]() 垂直平分线段
垂直平分线段![]() .
.
∴线段![]() 是
是![]() 中
中![]() 边上的高线.
边上的高线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户以1500元/亩的单价承包了15亩地种植板栗,每亩种植80株优质板栗嫁接苗,购买嫁接苗,购买价格为5元/株,且每亩地的管理费用为800元,一年下来喜获丰收平均每亩板栗产量为600kg,已知当地板栗的批发和;零售价格分别如下表所示:
销售方式 | 批发 | 零售 |
售价(元/kg) | 10 | 14 |
通过市场调研发现,批发与零售的总销量只能达到总产量的70%,其中零售量不高于总销售量的40%,经多方协调当地食品加工厂承诺以7元/kg的价格收购该农户余下的板栗,设板栗全部售出后的总利润为y元,其中零售x kg.
(1)求y与x之间的函数关系
(2)求该农户所收获的最大利润
(总利润=总销售额-总承包费用-购买板栗苗的费用-总管理费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况如下表:
颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
花朵数 | 1 | 2 | 3 | 4 | 5 | 6 |
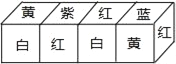
现将上述大小相同,颜色、花朵分布完全一样的四个正方体拼成一个在同一平面上放置的长方体,如图所示,那么长方体的下底面共有_____朵花.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A.
B.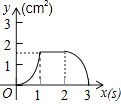
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:
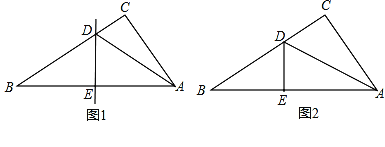
操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,可求得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为 ;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
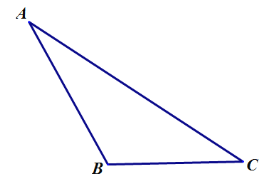
【题目】按照下列要求画图并填空:
(1)画出边![]() 的高,垂足为
的高,垂足为![]() ,则点
,则点![]() 到直线
到直线![]() 的距离是线段______的长.
的距离是线段______的长.
(2)用直尺和圆规作出![]() 的边
的边![]() 的垂直平分线
的垂直平分线![]() ,分别交直线
,分别交直线![]() 、
、![]() 于点
于点![]() 、
、![]() ,联结
,联结![]() ,则线段
,则线段![]() 是
是![]() 的______(保留作图痕迹).
的______(保留作图痕迹).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com