
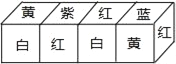
【题目】把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况如下表:
颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
花朵数 | 1 | 2 | 3 | 4 | 5 | 6 |
现将上述大小相同,颜色、花朵分布完全一样的四个正方体拼成一个在同一平面上放置的长方体,如图所示,那么长方体的下底面共有_____朵花.
【答案】17
【解析】
先根据图形得出最右边的正方体是:上蓝,下白,左绿,右红,前黄,后紫,即可推出其它正方形,判断出下面的颜色,代入朵数即可得出答案.
解:∵大小颜色花朵分布完全一样,
∴最左边的正方体告诉我们:黄色紧邻的面是白色;
最右边的正方体告诉我们:黄色紧邻着红色和蓝色;
∴可以推断出最右边的正方体的白色面是在它的左侧面或下底面;
又∵右数第二个正方体告诉我们红色紧邻着白色;
∴对于最右边的正方体,白色只可能在下底面(如果在左侧面就与红色是对立面了,不符题意);
∵根据左数第二个正方体可知:红色紧邻着紫色;
∴对于最右边的正方体,后侧面是紫色,左侧面是绿色.
即最右边的正方体为例,它是:上蓝,下白,左绿,右红,前黄,后紫.
也就是说:黄的对立面是紫;紫的对立面是黄;红的对立面是绿,蓝的对立面是白.
依次对应从左至右的四个正方体,下底面分别是:紫,黄,绿,白.
所以下面有花:5+2+6+4=17朵.
故答案为:17.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在直角坐标系中,A(0,4),C(2,0).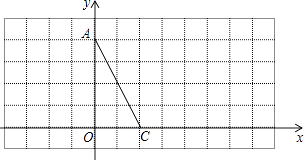
(1)画出线段AC关于y轴的对称线段AB;
(2)将线段CA绕点C顺时针旋转一个角,得到对应的线段CD,使得AD∥x轴,请画出线段CD;
(3)若直线y=kx平分四边形ABCD的面积,请求出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校创新能力大赛的笔试情况,随机抽查了部分参赛同学的成绩,整理井制作了不完整的统计表和统计图,请根据图表中提供的信息解答问题:
分数x(分) | 频数 | 百分比 |
60≤x<70 | 30 | 10% |
70≤x<80 | 90 | n |
80≤x<90 | m | 40% |
90≤x<100 | 60 | 20% |
(1)本次调查统计的学生人数为多少.
(2)在表中:写出m,n的值.
(3)补全频数分布直方图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图像与x轴交于A(-6,0)与y轴相交于点B,动点P从A出发,沿x轴向x轴的正方向运动.
的图像与x轴交于A(-6,0)与y轴相交于点B,动点P从A出发,沿x轴向x轴的正方向运动.
(1)求b的值,并求出△PAB为等腰三角形时点P的坐标;
(2)在点P出发的同时,动点Q也从点A出发,以每秒![]() 个单位的速度,沿射线AB运动,运动时间为t(s);
个单位的速度,沿射线AB运动,运动时间为t(s);
①点Q的坐标(用含t的表达式表示);
②若点P的运动速度为每秒k个单位,请直接写出当△APQ为等腰三角形时k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+4的图象与反比例函数y= ![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.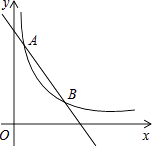
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
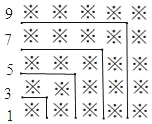
【题目】探索规律,观察下面由※组成的图案和算式,并解答问题.
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)试写出1+3+5+7+9+…+19= ;
(2)试写出1+3+5+7+9+…+(2n﹣1)= ;
(3)请用上述规律计算:
①101+103+105+107+…+2017+2019;
②(2m+1)+(2m+3)+(2m+5)+…+(2n+7)(其中n>m)(列出代数式即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα= ![]() ,则线段CE的最大值为 .
,则线段CE的最大值为 . 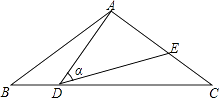
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com