
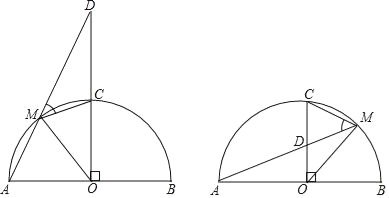
【题目】如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是![]() 上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
(1)若半圆的半径为10.
①当∠AOM=60°时,求DM的长;
②当AM=12时,求DM的长.
(2)探究:在点M运动的过程中,∠DMC的大小是否为定值?若是,求出该定值;若不是,请说明理由.
【答案】(1)①DM= 10;②MD=![]() ;(2)∠CMD=45°.
;(2)∠CMD=45°.
【解析】
(1)①当![]() 时,所以△AMO是等边三角形,从而可知∠MOD=30°,∠D=30°,所以DM=OM=10;
时,所以△AMO是等边三角形,从而可知∠MOD=30°,∠D=30°,所以DM=OM=10;
②过点M作MF⊥OA于点F,设AF=x,![]() 利用勾股定理即可求出x的值.易证明△AMF∽△ADO,从而可知AD的长度,进而可求出MD的长度.
利用勾股定理即可求出x的值.易证明△AMF∽△ADO,从而可知AD的长度,进而可求出MD的长度.
(2)根据点M的位置分类讨论,然后利用圆周角定理以及圆内接四边形的性质即可求出答案.
(1)①当∠AOM=60°时,
∵![]()
∴△AMO是等边三角形,
∴∠A=∠MOA=60°,
∴∠MOD=30°,∠D=30°,
∴DM=OM=10
②过点M作MF⊥OA于点F,
设![]()
∴![]()
∵![]()
由勾股定理可知:![]()
∴![]()
∴![]()
∵MF∥OD,
∴△AMF∽△ADO,
∴![]()
![]()
![]()
∴![]()
∴![]()
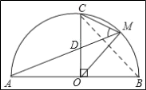
(2)当点M位于![]() 之间时,
之间时,
连接BC,
∵C是![]() 的中点,
的中点,
∴∠B=45°,
∵四边形AMCB是圆内接四边形,
此时∠CMD=∠B=45°,
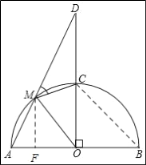
当点M位于![]() 之间时,
之间时,
连接BC,
由圆周角定理可知:∠CMD=∠B=45°
综上所述,∠CMD=45°


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
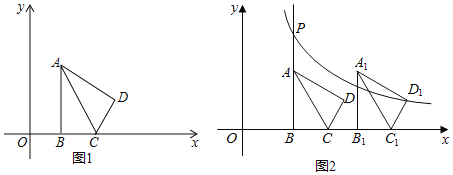
【题目】如图1,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限,B,C在x轴的正半轴上(C在B的右侧),BC=2,AB=2![]() ,△ADC与△ABC关于AC所在的直线对称.
,△ADC与△ABC关于AC所在的直线对称.
(1)当OB=2时,求点D的坐标;
(2)若点A和点D在同一个反比例函数的图象上,求OB的长;
(3)如图2,将第(2)题中的四边形ABCD向右平移,记平移后的四边形为A1B1C1D1,过点D1的反比例函数y=![]() (k≠0)的图象与BA的延长线交于点P.问:在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.
(k≠0)的图象与BA的延长线交于点P.问:在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红星中学九年级(1)班三位教师决定带领本班![]() 名学生利用假期去某地旅游,枫江旅行社的收费标准为:教师全价,学生半价;而东方旅行社不管教师还是学生一律八折优惠,这两家旅行社的全价都是500元。
名学生利用假期去某地旅游,枫江旅行社的收费标准为:教师全价,学生半价;而东方旅行社不管教师还是学生一律八折优惠,这两家旅行社的全价都是500元。
(1)用含![]() 的式子表示三位教师和
的式子表示三位教师和![]() 位学生参加这两家旅行社所需的费用各是多少元;
位学生参加这两家旅行社所需的费用各是多少元;
(2)如果![]() =50时,请你计算选择哪一家旅行社较为合算?
=50时,请你计算选择哪一家旅行社较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步深化基教育课程改革,构建符合素质教育要求的学校课程体系,某学校自主开发了A书法、B阅读,C足球,D器乐四门校本选修课程供学生选择,每门课程被选到的机会均等.
(1)学生小红计划选修两门课程,请写出所有可能的选法;
(2)若学生小明和小刚各计划送修一门课程,则他们两人恰好选修同一门课程的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
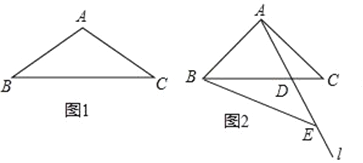
【题目】钝角三角形ABC中,∠BAC>90°,AB=AC,∠ACB=α,过点A的直线l交BC边于点D.点E在直线l上,且BC=BE.,点E在AD延长线上.
①当α=30°,点D恰好为BC中点时,补全图1直接写出∠BAE= °,
∠BEA= °;
②如图2,若∠BAE=2α,求∠BEA的度数(用含α的代数式表示);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店5月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.6月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店6月份购进这两种水果的数量与5月份都相同,将多支付货款300元,求该店5月份购进甲、乙两种水果分别是多少千克?
(2)若6月份将这两种水果进货总量减少到120千克,且甲种水果不超过乙种水果的3倍,则6月份该店需要支付这两种水果的货款最少应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
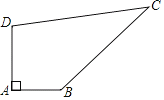
【题目】如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
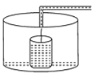
【题目】小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出无鱼水缸内最高水位![]() 与注水时间
与注水时间![]() 之间的变化情况的是( )
之间的变化情况的是( )
A. B.
B.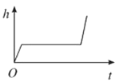
C.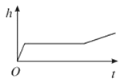 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
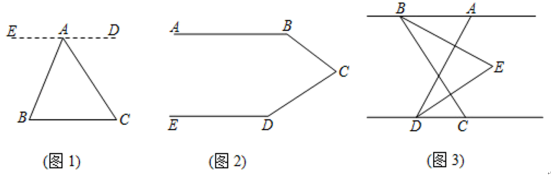
【题目】等角转化;如图1,已知点A是BC外一点,连结AB、AC,求∠BAC+∠B+∠C的度数.
(1)阅读并补充下面的推理过程
解:过点A作ED∥BC,
∴∠B=∠EAB,∠C= ( )
又∵∠EAB+∠BAC+∠DAC=180°
∴∠B+∠BAC+∠C=180°
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC、∠B、∠C“凑”在一起,得出角之间的关系,使问题得以解决.
(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数(提示:过点C作CF∥AB);
(3)如图3,已知AB∥CD,点C在点D的右侧,∠ADC=80°,点B在点A的左侧,∠ABC=60°,BE平分∠ABC,DE平分∠ADC,BE、DE所在的直线交于点E,点E在两条平行线AB与CD之间,求∠BED的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com