
【题目】某水果店5月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.6月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店6月份购进这两种水果的数量与5月份都相同,将多支付货款300元,求该店5月份购进甲、乙两种水果分别是多少千克?
(2)若6月份将这两种水果进货总量减少到120千克,且甲种水果不超过乙种水果的3倍,则6月份该店需要支付这两种水果的货款最少应是多少元?
【答案】(1)该店5月份购进甲种水果100千克,购进乙种水果50千克.(2)需要支付这两种水果的货款最少应是1500元.
【解析】
(1)设该店5月份购进甲种水果x千克,购进乙种水果y千克,根据总价=单价×购进数量,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购进甲种水果a千克,需要支付的货款为w元,则购进乙种水果(120﹣a)千克,根据总价=单价×购进数量,即可得出w关于a的函数关系式,由甲种水果不超过乙种水果的3倍,即可得出关于a的一元一次不等式,解之即可得出a的取值范围,再利用一次函数的性质即可解决最值问题.
(1)设该店5月份购进甲种水果x千克,购进乙种水果y千克,
根据题意得:![]() ,
,
解得:![]() ,
,
答:该店5月份购进甲种水果100千克,购进乙种水果50千克;
(2)设购进甲种水果a千克,需要支付的货款为w元,则购进乙种水果(120﹣a)千克,
根据题意得:w=10a+20(120﹣a)=﹣10a+2400,
∵甲种水果不超过乙种水果的3倍,
∴a≤3(120﹣a),
解得:a≤90,
∵k=﹣10<0,
∴w随a值的增大而减小,
∴当a=90时,w取最小值,最小值﹣10×90+2400=1500,
∴月份该店需要支付这两种水果的货款最少应是1500元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】问题情境:
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1,将矩形纸片![]() 沿对角线
沿对角线![]() 剪开,得到
剪开,得到![]() 和
和![]() .并且量得
.并且量得![]() ,
,![]() .
.
操作发现:
(1)将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转
为旋转中心,按逆时针方向旋转![]() ,使
,使![]() ,得到如图2所示的
,得到如图2所示的![]() ,过点
,过点![]() 作
作![]() 的平行线,与
的平行线,与![]() 的延长线交于点
的延长线交于点![]() ,则四边形
,则四边形![]() 的形状是________.
的形状是________.
(2)创新小组将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转,使
为旋转中心,按逆时针方向旋转,使![]() 、
、![]() 、
、![]() 三点在同一条直线上,得到如图3所示的
三点在同一条直线上,得到如图3所示的![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 并延长至点
并延长至点![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() ,得到四边形
,得到四边形![]() ,发现它是正方形,请你证明这个结论.
,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将![]() 沿着
沿着![]() 方向平移,使点
方向平移,使点![]() 与点
与点![]() 重合,此时
重合,此时![]() 点平移至
点平移至![]() 点,
点,![]() 与
与![]() 相交于点
相交于点![]() ,如图4所示,连接
,如图4所示,连接![]() ,试求
,试求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县木瓜村盛产优种红富士苹果,曾推选参加省农产品博览会,某人去该地水果批发市场采购苹果,他看中了A、B两家苹果.这两家苹果品质都一样,市场售价都为6元/千克,但批发进价不相同.两家苹果批发进价如下:
A家规定:批发数量不超过1000千克,可按市场售价的92%优惠;批发数量多于1000千克但不超过2000千克,可全部按市场售价的90%优惠;批发数超过2000千克则全部按市场售价的88%优惠.
B家的规定如下表:
数量范围(千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上部分 |
批发进价(元) | 市场售价的95% | 市场售价的85% | 市场售价的75% | 市场售价的70% |
[表格说明: ![]() 家苹果批发进价按分段计算,如:某人要批发苹果2100千克,则批发进价
家苹果批发进价按分段计算,如:某人要批发苹果2100千克,则批发进价![]() ]
]
根据上述信息,请解答下列问题:
(1)如果此人要批发1000千克苹果,则他在![]() 家批发需要_______元,在
家批发需要_______元,在![]() 家批发需要_______元;
家批发需要_______元;
(2)如果此人批发![]() 千克苹果(1500<x<2000),则他在
千克苹果(1500<x<2000),则他在![]() 家批发需要_______元,在
家批发需要_______元,在![]() 家批发需要_______元(用含
家批发需要_______元(用含![]() 的代数式表示);
的代数式表示);
(3)现在此人要批发3000千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我市将创建全国森林城市,提出了“共建绿色城”的倡议.某校积极响应,在3月12日植树节这天组织全校学生开展了植树活动,校团委对全校各班的植树情况道行了统计,绘制了如图所示的两个不完整的统计图.
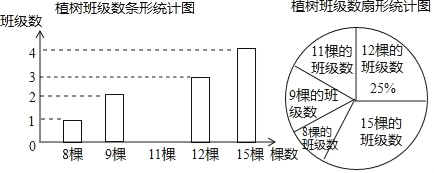
(1)求该校的班级总数;
(2)将条形统计图补充完整;
(3)求该校各班在这一活动中植树的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
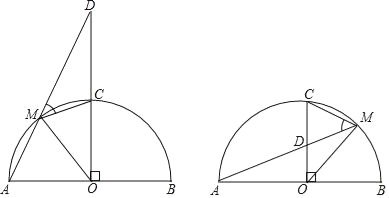
【题目】如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是![]() 上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
(1)若半圆的半径为10.
①当∠AOM=60°时,求DM的长;
②当AM=12时,求DM的长.
(2)探究:在点M运动的过程中,∠DMC的大小是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
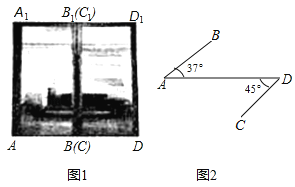
【题目】图1是一商场的推拉门,已知门的宽度![]() 米,且两扇门的大小相同(即
米,且两扇门的大小相同(即![]() ),将左边的门
),将左边的门![]() 绕门轴
绕门轴![]() 向里面旋转
向里面旋转![]() ,将右边的门
,将右边的门![]() 绕门轴
绕门轴![]() 向外面旋转
向外面旋转![]() ,其示意图如图2,求此时
,其示意图如图2,求此时![]() 与
与![]() 之间的距离(结果保留一位小数).(参考数据:
之间的距离(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:
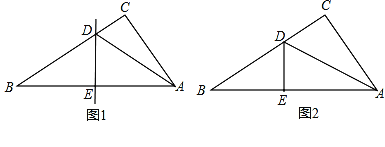
操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,可求得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为 ;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20m有一棵树C,继续前行20m到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米.
(1)河的宽度是 米.
(2)请你说明他们做法的正确性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB和CD相交于点O,OA是∠EOC的角平分线.
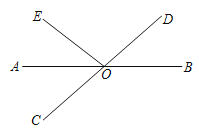
(1)若∠EOC=80°,求∠BOD的度数;
(2)∠EOC:∠EOD=2:3,求∠BOD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com