练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，直线AB和CD相交于点O，OA是∠EOC的角平分线．

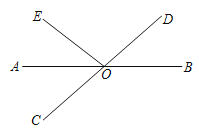
    （1）若∠EOC＝80°，求∠BOD的度数；

    （2）∠EOC：∠EOD＝2：3，求∠BOD的度数．

    【答案】（1）40°；（2）∠BOD＝36°

    【解析】

    （1）根据角平分线定义可得∠AOC＝∠AOE＝＝40°，再利用对顶角相等即可得出答案；

    （2）首先设∠EOC＝2x°，∠EOD＝3x°，根据邻补角互补可得方程，解方程可得x的值，进而可得答案．

    解：（1）∵OA是∠EOC的角平分线，

    ∴∠AOC＝∠AOE＝＝40°，

    ；

    （2）设∠EOC＝2x°，∠EOD＝3x°，

    ∴2x+3x＝180，

    ∴x＝36，

    ∴∠EOC＝72°，∠EOD＝108°，

    ∴∠AOC＝36°，

    ∴∠BOD＝36°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某水果店5月份购进甲、乙两种水果共花费1700元，其中甲种水果8元/千克，乙种水果18元/千克.6月份，这两种水果的进价上调为：甲种水果10元/千克，乙种水果20元/千克.

    （1）若该店6月份购进这两种水果的数量与5月份都相同，将多支付货款300元，求该店5月份购进甲、乙两种水果分别是多少千克？

    （2）若6月份将这两种水果进货总量减少到120千克，且甲种水果不超过乙种水果的3倍，则6月份该店需要支付这两种水果的货款最少应是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知中，，，点D为AB的中点．如果点P在线段BC上以2cm/s的速度由点B向C点运动，同时，点Q在线段AC上由点A向C点以4cm/s的速度运动．

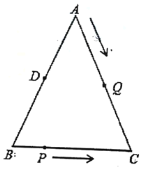
    （1）若点P、Q两点分别从B、A两点同时出发，经过2秒后，与是否全等？请说明理由；

    （2）若点P、Q两点分别从B、A两点同时出发，的周长为16cm，设运动时间为t，问：当t为何值时，是等腰三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在一条不完整的数轴上从左到右有三个点，其中点到点的距离为3，点到的距离为4设点所对应的数的和是

    (1)若以为原点，写出点所对应的数，并计算的值；若以为原点，求的值；

    (2)若原点在图中数轴上点的左侧，且点到原点的距离为1，求的值；

    (3)若原点在图中数轴上点的右侧，且点到点的距离为，求的值(用含的式子表示)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

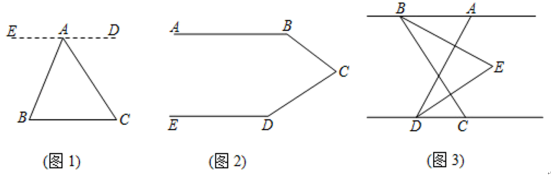
    【题目】等角转化；如图1，已知点A是BC外一点，连结AB、AC，求∠BAC+∠B+∠C的度数．

    （1）阅读并补充下面的推理过程

    解：过点A作ED∥BC，

    ∴∠B＝∠EAB，∠C＝　 　（　 　）

    又∵∠EAB+∠BAC+∠DAC＝180°

    ∴∠B+∠BAC+∠C＝180°

    从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将∠BAC、∠B、∠C“凑”在一起，得出角之间的关系，使问题得以解决．

    （2）如图2，已知AB∥ED，求∠B+∠BCD+∠D的度数（提示：过点C作CF∥AB）；

    （3）如图3，已知AB∥CD，点C在点D的右侧，∠ADC＝80°，点B在点A的左侧，∠ABC＝60°，BE平分∠ABC，DE平分∠ADC，BE、DE所在的直线交于点E，点E在两条平行线AB与CD之间，求∠BED的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】．Rt△ABC中，已知∠C＝90°，∠B＝50°，点D在边BC上，BD＝2CD（图4）．把△ABC绕着点D逆时针旋转m（0＜m＜180）度后，如果点B恰好落在初始Rt△ABC的边上，那么m＝_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知下列命题：①相等的角是对顶角；②互补的角就是平角；③互补的两个角一定是一个锐角，另一个为钝角：④平行于同一条直线的两直线平行；⑤两条平行线被第三条直线所截，同旁内角的角平分线互相垂直．其中，正确命题的个数为（ ）

    A.0B.1个C.2个D.3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

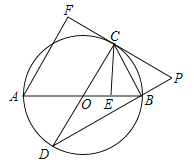
    【题目】（2017广东省）如图，AB是⊙O的直径，AB=，点E为线段OB上一点（不与O，B重合），作CE⊥OB，交⊙O于点C，垂足为点E，作直径CD，过点C的切线交DB的延长线于点P，AF⊥PC于点F，连接CB．

    （1）求证：CB是∠ECP的平分线；

    （2）求证：CF=CE；

    （3）当时，求劣弧的长度（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．

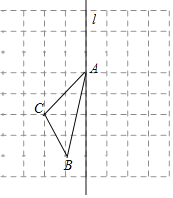
    （1）在图中画出与△ABC关于直线l成轴对称的△AB′C′；

    （2）在直线l上找一点P，使PB′+PC的长最短；

    （3）若△ACM是以AC为腰的等腰三角形，点M在小正方形的顶点上．这样的点M共有　 　个．

    查看答案和解析>>

    同步练习册答案