
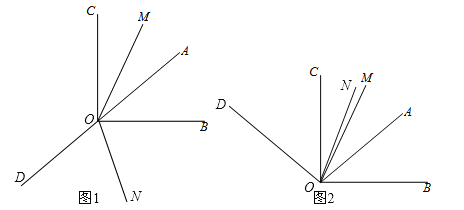
【题目】已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
(1)OA可能在∠BOD的内部,也可能在∠BOD的外部,请分两种情况,在下图中用直尺、量角器画出射线OD,ON的准确位置;
(2)当α=40°时,求(1)中∠MON的度数,要求写出计算过程;
(3)用含α的代数式表示∠MON的度数.(直接写出结果即可)

【答案】(1)详见解析;(2)∠MON=135°或5°;(3)∠MON=135°或45°﹣α.
【解析】
(1)分射线OA在∠BOD的外部和内部两种情况作出图形;
(2)根据互为余角和补角的定义求出∠AOC和∠BOD的度数,再根据角平分线的定义可得∠MOA=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,然后根据图形,分∠MON=∠MOA+∠AOB+∠BON和∠MON=∠NOB﹣∠MOA﹣∠AOB分别代入数据进行计算即可得解;
∠BOD,然后根据图形,分∠MON=∠MOA+∠AOB+∠BON和∠MON=∠NOB﹣∠MOA﹣∠AOB分别代入数据进行计算即可得解;
(3)分射线OA在∠BOD的外部和内部两种情况解答.
(1)如图1,图2所示;
(2)∵∠AOB=40°,∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,∴∠AOC=90°﹣∠AOB=50°,∠BOD=180°﹣∠AOB=140°.
∵OM平分∠AOC,ON平分∠BOD,∴∠MOA=![]() ∠AOC=
∠AOC=![]() ×50°=25°,∠BON=
×50°=25°,∠BON=![]() ∠BOD=
∠BOD=![]() ×140°=70°.
×140°=70°.
①如图1,∠MON=∠MOA+∠AOB+∠BON=25°+40°+70°=135°;
②如图2,∠MON=∠NOB﹣∠MOA﹣∠AOB=70°﹣25°﹣40°=5°;
∴∠MON=135°或5°;
(3)∠MON=135°或45°﹣α.


科目:初中数学 来源: 题型:
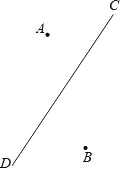
【题目】如图所示,李明和王丽家分别位于公路CD两侧的A,B处,星期天王丽要去为李明送书,他两人约定在公路CD边上见面.李明骑自行车,王丽步行,为节省时间,他们见面的地点定在距离王丽家最近的点E
(1)请你利用所学过的知识,画图确定点E的位置并写出画图依据;
(2)出门前李明发现自行车坏了,临时决定也步行前往,为节省时间,他们约定在距离他两家距离之和最小的F处见面,请你画出图形,确定点F的位置并写出画图依据.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a.
如:1☆3=1×32+2×1×3+1=16.
(1)求(﹣2)☆3的值;
(2)若(![]() ☆3)☆(﹣
☆3)☆(﹣![]() )=8,求a的值;
)=8,求a的值;
(3)若2☆x=m,(![]() x)☆3=n(其中x为有理数),试比较m,n的大小.
x)☆3=n(其中x为有理数),试比较m,n的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=130°,射线OC是∠AOB内部任意一条射线,OD、OE分别是∠AOC、∠BOC的角平分线,下列叙述正确的是( )
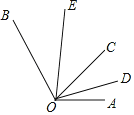
A. ∠DOE的度数不能确定 B. ∠AOD=![]() ∠EOC
∠EOC
C. ∠AOD+∠BOE=65° D. ∠BOE=2∠COD
查看答案和解析>>
科目:初中数学 来源: 题型:
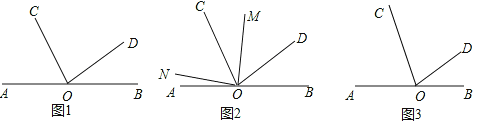
【题目】已知,点O是直线AB上一点,OC、OD为从点O引出的两条射线,∠BOD=30°,∠COD=![]() ∠AOC.
∠AOC.
(1)如图①,求∠AOC的度数;
(2)如图②,在∠AOD的内部作∠MON=90°,请直接写出∠AON与∠COM之间的数量关系 ;
(3)在(2)的条件下,若OM为∠BOC的角平分线,试说明∠AON=∠CON.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明设计了一个问题,分两步完成:
(1)已知关于x的一元一次方程![]() ,请画出数轴,并在数轴上标注a与
,请画出数轴,并在数轴上标注a与![]() 对应的点,分别记作A,B;
对应的点,分别记作A,B;
(2)在第1问的条件下,在数轴上另有一点C对应的数为y,C与A的距离是C与B的距离的5倍,且C在表示5的点的左侧,求y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC.请按下列要求解答:
(1)尺规作图:作∠BAC的角平分线交BC于点D,以AD为一边向右侧作等边△ADE(保留作图痕迹,不写作法).
(2)在(1)的图形上,设AC、DE交于点F,若CF=lcm,求△ABC的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com