
【题目】已知,点O是直线AB上一点,OC、OD为从点O引出的两条射线,∠BOD=30°,∠COD=![]() ∠AOC.
∠AOC.
(1)如图①,求∠AOC的度数;
(2)如图②,在∠AOD的内部作∠MON=90°,请直接写出∠AON与∠COM之间的数量关系 ;
(3)在(2)的条件下,若OM为∠BOC的角平分线,试说明∠AON=∠CON.
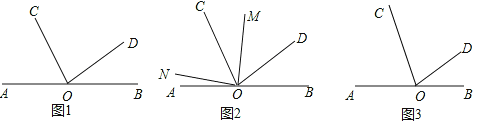
【答案】(1)∠AOC=70°;(2)∠AON+20°=∠COM;(3)详见解析.
【解析】
(1)由题意可知:∠AOD=∠AOC+∠COD,即∠AOC+![]() ∠AOC=150°,求解即可;
∠AOC=150°,求解即可;
(2)由角的和差关系即可得出结论;
(3)OM是∠BOC的角平分线,可以求出∠CON=∠MON﹣∠COM=35°,而∠AON=∠AOC﹣∠CON=35°,即可得出结论.
(1)由题意可知:∠AOB=180°,∠BOD=30°,∠AOD=∠AOB﹣∠BOD=150°.
∵∠AOD=∠AOC+∠COD,∠COD=![]() ∠AOC,∴∠AOC+
∠AOC,∴∠AOC+![]() ∠AOC=150°,∴∠AOC=70°;
∠AOC=150°,∴∠AOC=70°;
(2)∵∠AOC=70°,∴∠AON+∠NOC=70°①.
∵∠MON=90°,∠MOC+∠NOC=90°②,由①②可得:∠AON+20°=∠COM;
(3)∵∠AOC=70°,∠AOB=180°,∴∠BOC=∠AOB﹣∠AOC=110°.
∵OM是∠BOC的角平分线,∴∠COM=![]() ∠BOC=55°.
∠BOC=55°.
∵∠MON=90°,∴∠CON=∠MON﹣∠COM=35°.
∵∠AOC=70°,∴∠AON=∠AOC﹣∠CON=35°,∴∠AON=∠CON.


科目:初中数学 来源: 题型:
【题目】探究多边形内角和问题.
连接多边形不相邻的两个顶点的线段叫做多边形的对角线.从多边形某一个顶点出发的×对角线可以把一个多边形分成几个三角形.这样就把多边形内角和问题转化为三角形内角和问题了.
(1)请你试一试,做一做,把下面表格补充完整:
名称 | 图形 | 内角和 |
三角形 |
| 180° |
四边形 |
| 2×180°=360° |
五边形 |
|
|
六边形 |
|
|
… | … | … |
根据表格探究发现的规律,完成下面的问题:
(2)七边形的内角和等于 度;
(3)如果一个多边形有n条边,请你用含有n的代数式表示这个多边形的内角和: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
A. 矩形 B. 一组对边相等,另一组对边平行的四边形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨![]() 元收费
元收费![]() 如果超过20吨,未超过的部分按每吨
如果超过20吨,未超过的部分按每吨![]() 元收费,超过的部分按每吨
元收费,超过的部分按每吨![]() 元收费
元收费![]() 设某户每月用水量为x吨,应收水费为y元.
设某户每月用水量为x吨,应收水费为y元.
![]() 设某户居民每月用水量为m吨
设某户居民每月用水量为m吨![]() ,则应收水费为______元
,则应收水费为______元![]() 用含m的代数式表示
用含m的代数式表示![]() ;
;
![]() 设某户居民每月用水量为m吨
设某户居民每月用水量为m吨![]() ,则应收水费为______元
,则应收水费为______元![]() 用含m的代数式表示
用含m的代数式表示![]() ;
;
![]() 若该城市某户5月份水费平均为每吨
若该城市某户5月份水费平均为每吨![]() 元,求该户5月份用水多少吨?
元,求该户5月份用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
(1)OA可能在∠BOD的内部,也可能在∠BOD的外部,请分两种情况,在下图中用直尺、量角器画出射线OD,ON的准确位置;
(2)当α=40°时,求(1)中∠MON的度数,要求写出计算过程;
(3)用含α的代数式表示∠MON的度数.(直接写出结果即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD内放入六个小正方形后形成一个中心对称图形,其中顶点E、F分别在边BC、AD上,则长AD与宽AB的比值为( )
A.6:5
B.13:10
C.8:7
D.4:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和爸爸周末步行去游泳馆游冰,爸爸先出发了一段时间后小明才出发,途中小明在离家1400米处的报亭休息了一段时间后继续按原来的速度前往游泳馆.两人离家的距离y(米)与小明所走时间x(分钟)之间的函数关系如图所示,请结合图象信息解答下列问题:
(1)小明出发 分钟后第一次与爸爸相遇;
(2)分别求出爸爸离家的距离y1和小明到达报亭前离家的距离y2与时间x之间的函数关系式;
(3)求小明在报亭休息了多长时间遇到姗姗来迟的爸爸;
(4)若游泳馆离小明家2000米,请你通过计算说明谁先到达游泳馆.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D。AF平分∠CAB,交CD于点E,交CB于点F。

(1)求证:CE=CF。
(2)将图(1)中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其它条件不变,如图(2)所示。试猜想:BE′与CF有怎样的数量关系?请证明你的结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com