
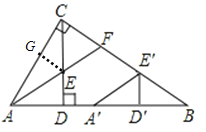
【题目】如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D。AF平分∠CAB,交CD于点E,交CB于点F。

(1)求证:CE=CF。
(2)将图(1)中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其它条件不变,如图(2)所示。试猜想:BE′与CF有怎样的数量关系?请证明你的结论。
【答案】(1)见解析证明;(2)![]() =CF.理由见解析证明.
=CF.理由见解析证明.
【解析】
试题分析:(1)根据角平分线的定义可得∠CAF=∠EAD,再根据等角的余角相等求出∠CFA=∠AED ,然后根据对顶角相等可得∠AED=∠CEF,从而得到∠CFA=∠AED,再根据等角对等边证明即可;(2)过点E作EG⊥AC于点G,根据角平分线的性质得到ED=EG,根据平移的性质可得![]() =DE,然后求出∠ACD=∠B,再利用“角角边”证明△CEG≌
=DE,然后求出∠ACD=∠B,再利用“角角边”证明△CEG≌![]() 全等,根据全等三角形对应边相等可得BE′=CE,从而得到BE′=CF.
全等,根据全等三角形对应边相等可得BE′=CE,从而得到BE′=CF.
试题解析:(1)∵AF平分∠CAB,∴∠CAF=∠EAD,∵∠ACB=90°,∴∠CAF+∠CFA=90°,∵CD⊥AB,∴∠EAD+∠AED=90°, ∴∠CFA=∠AED ,又∵∠AED=∠CEF,∴∠CFA=∠AED,∴CE=CF;
(2)答:![]() =CF. 过点E作EG⊥AC于点G,
=CF. 过点E作EG⊥AC于点G,
∵AF平分∠CAB,ED⊥AB,EG⊥AC,∴ED=EG,∵△ADE平移得到![]() ,∴
,∴![]() =DE,∴
=DE,∴![]() =GE,∵∠ACB=90°,∴∠ACD+∠DCB=90°,∵CD⊥AB,∴∠B+∠DCB=90°,∴∠ACD=∠B,在△CEG和
=GE,∵∠ACB=90°,∴∠ACD+∠DCB=90°,∵CD⊥AB,∴∠B+∠DCB=90°,∴∠ACD=∠B,在△CEG和![]() 中,∵
中,∵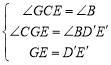 ,∴△CEG≌
,∴△CEG≌![]() (AAS),∴CE=
(AAS),∴CE=![]() ,又∵CE=CF,∴
,又∵CE=CF,∴![]() =CF.
=CF.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
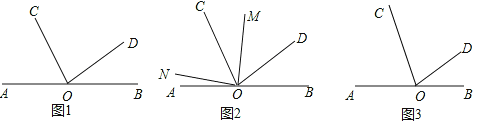
【题目】已知,点O是直线AB上一点,OC、OD为从点O引出的两条射线,∠BOD=30°,∠COD=![]() ∠AOC.
∠AOC.
(1)如图①,求∠AOC的度数;
(2)如图②,在∠AOD的内部作∠MON=90°,请直接写出∠AON与∠COM之间的数量关系 ;
(3)在(2)的条件下,若OM为∠BOC的角平分线,试说明∠AON=∠CON.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线.若OC是∠AOD的平分线,则∠BOC=_____°,射线OC的方向是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一组数,按照下列规律排列:
1,
2,3,
6,5,4,
7,8,9,10,
15,14,13,12,11,
16,17,18,19,20,21,
……
数字5在第三行左数第二个,我们用(3,2)点示5的位置,那点这组成数里的数字100的位置可以表示为( )
A. (14,9) B. (14,10) C. (14,11) D. (14,12)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为4,△ABC的顶点都在格点.
(1)求每个小矩形的长与宽;
(2)在矩形网格中找出所有的格点E,使△ABE为直角三角形;(描出相应的点,并分别用E1 , E2…表示)
(3)求sin∠ACB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( ) 
A.20 ![]()
B.25 ![]()
C.30 ![]()
D.40 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB. 
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长和扇形DOE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com