Question

【题目】在矩形ABCD中，∠ABC的平分线交AD于点E，∠BED的平分线交DC于点F，若AB=6，点F恰为DC的中点，则BC=（结果保留根号）

Answer 1

【答案】3+3
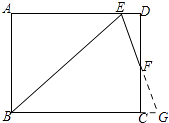
【解析】解：延长EF和BC，交于点G，如图所示： ∵矩形ABCD中，∠B的角平分线BE与AD交于点E，
∴∠ABE=∠AEB=45°，
∴AB=AE=6，
∴等腰直角△ABE中，BE= =6 ，
又∵∠BED的角平分线EF与DC交于点F，
∴∠BEG=∠DEF
∵AD∥BC
∴∠G=∠DEF
∴∠BEG=∠G
∴BG=BE=6 ，
∵∠G=∠DEF，∠EFD=∠GFC，
∴△EFD∽△GFC
∴ =1，
∴CG=DE，
设CG=DE=x，则AD=6+x=BC，
∵BG=BC+CG，
∴6 =6+x+x，
解得：x=3 ﹣3
∴BC=6+（3 ﹣3）=3+3 ；
故答案为：3+3 ．

先延长EF和BC，交于点G，再根据条件可以判断三角形ABE为等腰直角三角形，并求得其斜边BE的长，然后根据条件判断三角形BEG为等腰三角形，最后根据△EFD∽△GFC得出CG与DE的相等关系，并根据BG=BC+CG进行计算即可．