
【题目】解下列方程:
(1)4-![]() m=-m; (2)56-8x=11+x;
m=-m; (2)56-8x=11+x;
(3) ![]() x+1=5+
x+1=5+![]() x; (4)-5x+6+7x=1+2x-3+8x.
x; (4)-5x+6+7x=1+2x-3+8x.
【答案】(1) m=-10;(2)x=5;(3)x=4;(4)x=1.
【解析】试题分析:(1)移项、合并同类项后,系数化为1即可得方程的解;(2)移项、合并同类项后,系数化为1即可得方程的解;(3)移项、合并同类后项即可得方程的解;(4)移项、合并同类项后,系数化为1即可得方程的解.
试题解析:
(1) 移项,得-![]() m+m=-4.
m+m=-4.
合并同类项,得![]() m=-4.
m=-4.
系数化为1,得m=-10.
(2) 移项,得-8x-x=11-56.
合并同类项,得-9x=-45.
系数化为1,得x=5.
(3) 移项,得![]() x-
x-![]() x=5-1.
x=5-1.
合并同类项,得x=4.
(4) 移项,得-5x+7x-2x-8x=1-3-6.
合并同类项,得-8x=-8.
系数化为1,得x=1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1.
(1)如果点 A,D 表示的数互为相反数,那么点B表示的数是多少?
(2)如果点B,D表示的数互为相反数,那么图中表示的四个点中,哪一点表示的数的绝对值最大?为什么?
(3)当点B为原点时,若存在一点M到A的距离是点M到D的距离的2倍,则点M所表示的数是多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
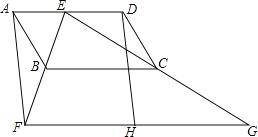
【题目】如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使![]() ,连接EC并延长,使
,连接EC并延长,使![]() ,连接
,连接![]() 为FG的中点,连接DH.
为FG的中点,连接DH.
![]() 求证:四边形AFHD为平行四边形;
求证:四边形AFHD为平行四边形;
![]() 若
若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4(k﹣![]() )=0.
)=0.
(1)判断这个一元二次方程的根的情况;
(2)若等腰三角形的一边长为3,另两条边的长恰好是这个方程的两个根,求这个等腰三角形的周长及面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
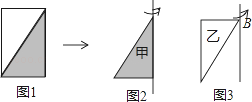
【题目】如图1,把一张长10厘米、宽6厘米的长方形纸板分成两个相同的直角三角形.
(1)甲三角形(如图2)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方米?
(2)乙三角形(如图3)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E. 
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB=°时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古籍《周髀算经》中早有记载“勾三股四弦五”,下面我们来探究两类特殊的勾股数.通过观察完成下面两个表格中的空格(以下a、b、c为Rt△ABC的三边,且a<b<c):
表一 表二
a | b | c | a | b | c | |
3 | 4 | 5 | 6 | 8 | 10 | |
5 | 12 | 13 | 8 | 15 | 17 | |
7 | 24 | 25 | 10 | 24 | 26 | |
9 | 41 | 12 | 37 |
(1)仔细观察,表一中a为大于1的奇数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(2)仔细观察,表二中a为大于4的偶数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(3)我们还发现,表一中的三边长“3,4,5”与表二中的“6,8,10”成倍数关系,表一中的“5,12,13”与表二中的“10,24,26”恰好也成倍数关系……请直接利用这一规律计算:在Rt△ABC中,当![]() ,
,![]() 时,斜边c的值.
时,斜边c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com