
【题目】已知:如图,ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E. 
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB=°时,四边形ACED是正方形?请说明理由.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠D=∠OCE,∠DAO=∠E.
∵O是CD的中点,
∴OC=OD,
在△ADO和△ECO中,
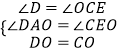 ,
,
∴△AOD≌△EOC(AAS);
(2)45
【解析】(2)当∠B=∠AEB=45°时,四边形ACED是正方形. ∵△AOD≌△EOC,
∴OA=OE.
又∵OC=OD,
∴四边形ACED是平行四边形.
∵∠B=∠AEB=45°,
∴AB=AE,∠BAE=90°.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠COE=∠BAE=90°.
∴ACED是菱形.
∵AB=AE,AB=CD,
∴AE=CD.
∴菱形ACED是正方形.
所以答案是:45.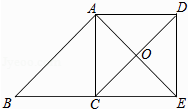
【考点精析】根据题目的已知条件,利用平行四边形的性质和正方形的判定方法的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】某手机经销商计划同时购进一批甲、乙两种型号的手机,若购进2部甲型号手机和1部乙型号手机,共需要资金2800元;若购进3部甲型号手机和2部乙型号手机,共需要资金4600元
(1) 求甲、乙型号手机每部进价为多少元?
(2) 该店计划购进甲、乙两种型号的手机销售,预计用不多于1.8万元且不少于1.74万元的资金购进这两部手机共20台,请问有几种进货方案?请写出进货方案
(3) 售出一部甲种型号手机,利润率为40%,乙型号手机的售价为1280元.为了促销,公司决定每售出一台乙型号手机,返还顾客现金m元,而甲型号手机售价不变,要使(2)中所有方案获利相同,求m的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答后面的问题。
我们知道方程![]() 有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由
有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由![]() ,得
,得![]() ,(
,( ![]() 、
、![]() 为正整数)
为正整数)
![]() 则有
则有![]() .又
.又![]() 为正整数,则
为正整数,则![]() 为整数.
为整数.
由2与3互质,可知: ![]() 为3的倍数,从而
为3的倍数,从而![]() ,代入
,代入![]() .
.
![]() 的正整数解为
的正整数解为![]()
问题:(1)若![]() 为自然数,则满足条件的
为自然数,则满足条件的![]() 值有_____________个
值有_____________个
(2)请你写出方程![]() 的所有正整数解:_________________________
的所有正整数解:_________________________
(3)若![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,并求出它的所有整数解。
,并求出它的所有整数解。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)﹣6﹣8+5﹣(﹣2);
(2)(﹣49)﹣(+91)﹣(﹣5)+(﹣9);
(3)![]() ;
;
(4)(![]() )×(﹣24);
)×(﹣24);
(5)(﹣3.59)×(![]() )﹣2.41×(
)﹣2.41×(![]() )+6×(
)+6×(![]() );
);
(6)﹣23+|2﹣3|﹣2×(﹣1)2014.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两台机器加工相同的零件,甲机器加工160个零件所用的时间与乙机器加工120个零件所用的时间相等.已知甲、乙两台机器每小时共加工35个零件,求甲、乙两台机器每小时各加工多少个零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
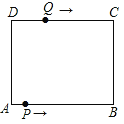
【题目】如图在长方形ABCD中,AB=12cm,BC=8cm,点P从A点出发,沿A→B→C→D路线运动,到D点停止;点Q从D点出发,沿D→C→B→A运动,到A点停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,用x(秒)表示运动时间.
(1)求点P和点Q相遇时的x值.
(2)连接PQ,当PQ平分矩形ABCD的面积时,求运动时间x值.
(3)若点P、点Q运动到6秒时同时改变速度,点P的速度变为每秒3cm,点Q的速度为每秒1cm,求在整个运动过程中,点P、点Q在运动路线上相距路程为20cm时运动时间x值.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com