
【题目】阅读下列材料,然后解答后面的问题。
我们知道方程![]() 有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由
有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由![]() ,得
,得![]() ,(
,( ![]() 、
、![]() 为正整数)
为正整数)
![]() 则有
则有![]() .又
.又![]() 为正整数,则
为正整数,则![]() 为整数.
为整数.
由2与3互质,可知: ![]() 为3的倍数,从而
为3的倍数,从而![]() ,代入
,代入![]() .
.
![]() 的正整数解为
的正整数解为![]()
问题:(1)若![]() 为自然数,则满足条件的
为自然数,则满足条件的![]() 值有_____________个
值有_____________个
(2)请你写出方程![]() 的所有正整数解:_________________________
的所有正整数解:_________________________
(3)若![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,并求出它的所有整数解。
,并求出它的所有整数解。
【答案】 (1)4 (2) ![]() ,
, ![]() ) (3)
) (3) ![]()
![]()
![]()
![]()
【解析】根据已知代数式为自然数,确定出x的值即可;
(2)用x表示出y,确定出方程的正整数解即可;
(3)用x表示出y,确定出方程的整数解即可.
解:(1)由题意得:x2=1,x2=2,x2=3,x2=6,
解得:x=3,x=4,x=5,x=8,共4个;
故答案为:4;
(2)方程整理得:y=2x+5,
当x=1时,y=3;当x=2时,y=1,
则方程的正整数解为![]() ,
, ![]() ;
;
故答案为: ![]() ,
, ![]()
(3)根据题意得:y=![]() ,
,
根据题意得:x+3=1,x+3=2,x+3=4,x+3=8,
解得:x=2,x=1,x=1,x=5,
相应的y=8,y=4,y=2,y=1,
∴它的所有整数解为![]()
![]()
![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】手机微信推出了抢红包游戏,它有多种玩法,其中一种为“拼手气红包”,用户设定好总金额以及红包个数后,可以生成不等金额的红包.现有一用户发了三个“拼手气红包”,总金额为3元,随机被甲、乙、丙三人抢到.
(1)判断下列事件中,哪些是确定事件,哪些是不确定事件?
①丙抢到金额为1元的红包;
②乙抢到金额为4元的红包
③甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多;
(2)记金额最多、居中、最少的红包分别为A,B,C.
①求出甲抢到红包A的概率;
②若甲没抢到红包A,则乙能抢到红包A的概率又是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA∥射线CB,∠C=∠OAB=100°.点D、E在线段CB上,且∠DOB=∠BOA,OE平分∠DOC.
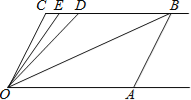
(1)试说明AB∥OC的理由;
(2)试求∠BOE的度数;
(3)平移线段AB;
①试问∠OBC:∠ODC的值是否会发生变化?若不会,请求出这个比值;若会,请找出相应变化规律.
②若在平移过程中存在某种情况使得∠OEC=∠OBA,试求此时∠OEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使![]() ,连接EC并延长,使
,连接EC并延长,使![]() ,连接
,连接![]() 为FG的中点,连接DH.
为FG的中点,连接DH.
![]() 求证:四边形AFHD为平行四边形;
求证:四边形AFHD为平行四边形;
![]() 若
若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
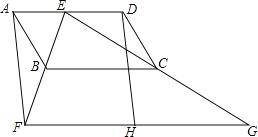
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4(k﹣![]() )=0.
)=0.
(1)判断这个一元二次方程的根的情况;
(2)若等腰三角形的一边长为3,另两条边的长恰好是这个方程的两个根,求这个等腰三角形的周长及面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E. 
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB=°时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°. 
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为4,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com