
【题目】如图,射线OA∥射线CB,∠C=∠OAB=100°.点D、E在线段CB上,且∠DOB=∠BOA,OE平分∠DOC.
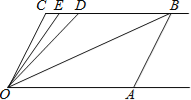
(1)试说明AB∥OC的理由;
(2)试求∠BOE的度数;
(3)平移线段AB;
①试问∠OBC:∠ODC的值是否会发生变化?若不会,请求出这个比值;若会,请找出相应变化规律.
②若在平移过程中存在某种情况使得∠OEC=∠OBA,试求此时∠OEC的度数.
【答案】(1)理由见解析(2)40°(3)①1:2②60°
【解析】试题分析:(1)根据OA//CB,得出![]() ,再根据已知条件,即可证明∠C+∠ABC=180°,从而得证.(2)根据两直线平行,同旁内角互补求出∠AOC,再求出∠EOB=
,再根据已知条件,即可证明∠C+∠ABC=180°,从而得证.(2)根据两直线平行,同旁内角互补求出∠AOC,再求出∠EOB=![]() ∠AOC.(3)①根据两直线平行,内错角相等可得∠AOB=∠OBC,再根据三角形的外角性质∠OEC=2∠OBC即可.②根据三角形的内角定理,求出∠COE=∠AOB,从而得到OB、OD、OE是∠AOC的四等分线,在利用三角形的内角定理即可求出∠OEC的度数.
∠AOC.(3)①根据两直线平行,内错角相等可得∠AOB=∠OBC,再根据三角形的外角性质∠OEC=2∠OBC即可.②根据三角形的内角定理,求出∠COE=∠AOB,从而得到OB、OD、OE是∠AOC的四等分线,在利用三角形的内角定理即可求出∠OEC的度数.
试题解析:(1)∵OA∥CB,∴∠OAB+∠ABC=180°,∵∠C=∠OAB=100°,∴∠C+∠ABC=180°,
∴AB∥OC . (2)∵CB∥OA,∴∠AOC=180°﹣∠C=180°﹣100°=80°,∵OE平分∠COD,∴∠COE=∠EOD,∵∠DOB=∠AOB,∴∠EOB=∠EOD+∠DOB=![]() ∠AOC=
∠AOC=![]() ×80°=40°;(3)①∵CB∥OA,∴∠AOB=∠OBC,∵∠EOB=∠AOB,∴∠EOB=∠OBC,∴∠OEC=∠EOB+∠OBC=2∠OBC,∴∠OBC:∠OEC=1:2,是定值;
×80°=40°;(3)①∵CB∥OA,∴∠AOB=∠OBC,∵∠EOB=∠AOB,∴∠EOB=∠OBC,∴∠OEC=∠EOB+∠OBC=2∠OBC,∴∠OBC:∠OEC=1:2,是定值;
②在△COE和△AOB中,∵∠OEC=∠OBA,∠C=∠OAB,∴∠COE=∠AOB,∴OB、OD、OE是∠AOC的四等分线,
∴∠COE=![]() ∠AOC=
∠AOC=![]() ×80°=20°,∴∠OEC=180°﹣∠C﹣∠COE=180°﹣100°﹣20°=60°,∴∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
×80°=20°,∴∠OEC=180°﹣∠C﹣∠COE=180°﹣100°﹣20°=60°,∴∠OEC=∠OBA,此时∠OEC=∠OBA=60°.


科目:初中数学 来源: 题型:
【题目】 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E. 
(1)求证:AC平分∠DAB;
(2)若∠B=60°,CD=2 ![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC、BC边上运动,且保持AD=CE,连接DE,DF,EF,在此运动过程中,下列结论:(1)△DFE是等腰直角三角形;(2)DE长度的最小值为4;(3)四边形CDFE的面积保持不变;(4)△CDE面积的最大值是4.正确的结论是( )

A. (1)(2)(3) B. (1)(3)(4) C. (1)(2)(4) D. (2)(3)(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,抛物线y=ax2+x的对称轴为直线x=2,顶点为A.点P为抛物线对称轴上一点,连结OA、OP.当OA⊥OP时,P点坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C是AB的中点,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为x秒(x>0).
(1)当x= 秒时,点P到达点A;
(2)运动过程中点P表示的数是 (用含x的代数式表示);
(3)当P,C之间的距离为2个单位长度时,求x的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答后面的问题。
我们知道方程![]() 有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由
有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由![]() ,得
,得![]() ,(
,( ![]() 、
、![]() 为正整数)
为正整数)
![]() 则有
则有![]() .又
.又![]() 为正整数,则
为正整数,则![]() 为整数.
为整数.
由2与3互质,可知: ![]() 为3的倍数,从而
为3的倍数,从而![]() ,代入
,代入![]() .
.
![]() 的正整数解为
的正整数解为![]()
问题:(1)若![]() 为自然数,则满足条件的
为自然数,则满足条件的![]() 值有_____________个
值有_____________个
(2)请你写出方程![]() 的所有正整数解:_________________________
的所有正整数解:_________________________
(3)若![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,并求出它的所有整数解。
,并求出它的所有整数解。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆统景温泉风景区被喻为“巴渝十二景”.为丰富旅游配套资源,镇政府决定大力发动农户扩大柑橘和蔬菜种植面积,并取得了较好的经济效益.今年该镇柑橘和蔬菜的收成比去年增加了80吨,其中柑橘的收成比去年增加了20%,蔬菜的收成比去年增加了30%,从而使今年的收成共达到了420吨.
(1)统景镇去年柑橘和蔬菜的收成各是多少吨?
(2)由于今年大丰收,镇政府计划用甲、乙两种货车共33辆将柑橘和蔬菜一次性运去参加渝洽会.已知一辆甲种货车最多可装13吨柑橘和3吨蔬菜;一辆乙种货车最多可装柑橘5吨和蔬菜6吨,安排甲、乙两种货车共有几种方案?
(3)若甲种货车的运费为每辆600元,乙种货车的运费为每辆500元,在(2)的情况下,如何安排运费最少,最少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,相距5km的A、B两地间有一条笔直的马路,C地位于AB两地之间且距A地2km,小明同学骑自行车从A地出发沿马路以每小时5km的速度向B地匀速运动,当到达B地后立即以原来的速度返回。到达A地停止运动,设运动时间为t(小时).小明的位置为点P、若以点C为坐标原点,以从A到B为正方向,用1个单位长度表示1km,解答下列各问:
![]()
(1)指出点A所表示的有理数;
(2)求t =0.5时,点P表示的有理数;
(3)当小明距离C地1km时,直接写出所有满足条件的t值;
(4)在整个运动过程中,求点P与点A的距离(用含t的代数式表示);
(5)用含t的代数式表示点P表示的有理数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com