
【题目】已知:如图,在平面直角坐标系中,抛物线y=ax2+x的对称轴为直线x=2,顶点为A.点P为抛物线对称轴上一点,连结OA、OP.当OA⊥OP时,P点坐标为 . 
【答案】(2,﹣4)
【解析】解:∵抛物线y=ax2+x的对称轴为直线x=2, ∴﹣ ![]() =2,
=2,
∴a=﹣ ![]() ,
,
∴抛物线的表达式为:y=﹣ ![]() x2+x,
x2+x,
∴顶点A的坐标为(2,1),
设对称轴与x轴的交点为E.
如图,在直角三角形AOE和直角三角形POE中,tan∠OAE= ![]() ,tan∠EOP=
,tan∠EOP= ![]() ,
,
∵OA⊥OP,
∴∠OAE=∠EOP,
∴ ![]() =
= ![]() ,
,
∵AE=1,OE=2,
∴ ![]() =
= ![]() ,
,
解得PE=4,
∴P(2,﹣4),
所以答案是:(2,﹣4).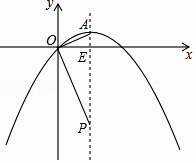
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
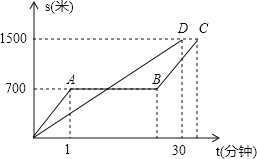
(1)填空:折线OABC表示赛跑过程中 的路程与时间的关系,线段OD表示赛跑过程中 的路程与时间的关系.赛跑的全程是 米.
(2)兔子在起初每分钟跑 米,乌龟每分钟爬 米.
(3)乌龟用了 分钟追上了正在睡觉的兔子.
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,每个小正方形的边长为一个单位长度.已知△ABC的顶点A(-2,5)、B(-4,1)、C(2,3),将△ABC平移得到△A′B′C′,点A(a,b)对应点A′(a+3,b-4)
(1) 画出△A′B′C′并写出点B′、C′的坐标
(2) 试求线段AB在整个平移的过程中在坐标平面上扫过的面积
(3) 在x轴上存在一点P,使得S△ABP=6,则点P的坐标是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机微信推出了抢红包游戏,它有多种玩法,其中一种为“拼手气红包”,用户设定好总金额以及红包个数后,可以生成不等金额的红包.现有一用户发了三个“拼手气红包”,总金额为3元,随机被甲、乙、丙三人抢到.
(1)判断下列事件中,哪些是确定事件,哪些是不确定事件?
①丙抢到金额为1元的红包;
②乙抢到金额为4元的红包
③甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多;
(2)记金额最多、居中、最少的红包分别为A,B,C.
①求出甲抢到红包A的概率;
②若甲没抢到红包A,则乙能抢到红包A的概率又是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA∥射线CB,∠C=∠OAB=100°.点D、E在线段CB上,且∠DOB=∠BOA,OE平分∠DOC.
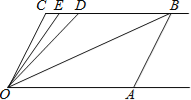
(1)试说明AB∥OC的理由;
(2)试求∠BOE的度数;
(3)平移线段AB;
①试问∠OBC:∠ODC的值是否会发生变化?若不会,请求出这个比值;若会,请找出相应变化规律.
②若在平移过程中存在某种情况使得∠OEC=∠OBA,试求此时∠OEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4(k﹣![]() )=0.
)=0.
(1)判断这个一元二次方程的根的情况;
(2)若等腰三角形的一边长为3,另两条边的长恰好是这个方程的两个根,求这个等腰三角形的周长及面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形纸片ABCD的边长为4cm,点M、N分别在边AB、CD上.将该纸片沿MN折叠,使点D落在边BC上,落点为E,MN与DE相交于点Q.随着点M的移动,点Q移动路线长度的最大值是____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com