
【题目】已知抛物线y=﹣![]() x2+bx+4与x轴相交于AB两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
x2+bx+4与x轴相交于AB两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
(1)求抛物线的表达式及它的对称轴方程;
(2)求点C的坐标,并求线段BC所在直线的函数表达式;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
【答案】(1)抛物线解析式为 ![]() 对称轴方程为:
对称轴方程为:![]() ;(2)点C的坐标为(0,4),直线BC的解析式为
;(2)点C的坐标为(0,4),直线BC的解析式为![]() ;(3)存在点Q,使
;(3)存在点Q,使![]() 为等腰三角形,点Q的坐标为:
为等腰三角形,点Q的坐标为:![]()
![]() .
.
【解析】
试题分析:(1)利用待定系数法求出抛物线解析式,利用配方法或公式法![]() 求出对称轴方程;
求出对称轴方程;
在抛物线解析式中,令![]() ,可求出点C的坐标,令
,可求出点C的坐标,令![]() ,可求出点B的坐标,再利用待定系数法求出直线BC的解析式;
,可求出点B的坐标,再利用待定系数法求出直线BC的解析式;
本问为存在型问题.若![]() 为等腰三角形,则有三种可能的情况,需要分类讨论,逐一计算.
为等腰三角形,则有三种可能的情况,需要分类讨论,逐一计算.
试题解析:
∵抛物线![]() 的图象经过点A(-2,0),
的图象经过点A(-2,0),![]() ,解得
,解得![]()
∴抛物线解析式为 ![]() 又∵
又∵![]() ∴对称轴方程为:
∴对称轴方程为:![]()
(2)在![]() 中,令
中,令![]() ,得
,得![]() ,∴C(0,4);令
,∴C(0,4);令![]() ,即
,即![]() ,整理得
,整理得![]() 解得:
解得:![]() ∴A(-2,0),B(8,0).设直线BC的解析式为
∴A(-2,0),B(8,0).设直线BC的解析式为![]() ,把B(8,0),C(0,4)的坐标分别代入解析式,得:
,把B(8,0),C(0,4)的坐标分别代入解析式,得:![]() ,解得
,解得 ,直线BC的解析式为
,直线BC的解析式为![]()
(3)∵抛物线的对称轴方程为:![]() 可设点Q(3,t),则可求得:
可设点Q(3,t),则可求得:![]()
![]()
![]() ①当
①当![]() 时,有
时,有![]() 解得
解得![]() ∴
∴![]() ②当
②当![]() 时,有
时,有![]() 此方程无实数根,∴此时
此方程无实数根,∴此时![]() 不能构成等腰三角形;当
不能构成等腰三角形;当![]() 时,有
时,有![]() 解得:
解得:![]() ∴点Q坐标为:
∴点Q坐标为:![]() .综上所述,存在点Q,使
.综上所述,存在点Q,使![]() 为等腰三角形,点Q的坐标为:
为等腰三角形,点Q的坐标为:![]()
![]() .
.


科目:初中数学 来源: 题型:
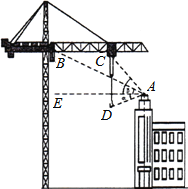
【题目】为了给学生提供更好的学习生活环境,重庆一中寄宿学校2015年对校园进行扩建.某天一台塔吊正对新建教学楼进行封顶施工,工人在楼顶A处测得吊钩D处的俯角α=22°,测得塔吊B,C两点的仰角分别为β=27°,γ=50°,此时B与C距3米,塔吊需向A处吊运材料.(tan27°≈0.5,tan50°≈1.2,tan22°≈0.4)
(1)吊钩需向右、向上分别移动多少米才能将材料送达A处?
(2)封顶工程完毕后需尽快完成新建教学楼的装修工程.如果由甲、乙两个工程队合做,12天可完成;如果由甲、乙两队单独做,甲队比乙队少用10天完成.求甲、乙两工程队单独完成此项工程所需的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列由左边到右边的变形中,因式分解正确的是( )
A. x2+3x-4=x(x+3) B. x2-4+3x=(x+2)(x-2) C. x2-4=(x+2)(x-2) D. x2-2xy+4y2=(x-y)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,
(1)每轮感染中平均一台电脑会感染几台电脑?
(2)若该病毒得不到有效控制,第3轮感染后,被感染的电脑会不会超过700台?说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段EF是由线段PQ平移得到的,点P(-1,4)的对应点为E(4,7),则点Q(-3,1)的对应点F的坐标为( )
A. (-8,-2) B. (-2,2) C. (2,4) D. (-6,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为9cm的等边三角形ABC中,D为BC上一点,且BD=3cm,E在AC上,∠ADE=60°,则AE的长为( )

A.2cm B.5cm C.6cm D.7cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种生物细胞的半径约为0.00028m,将0.00028用科学记数法表示为( )
A.0.28×10﹣3 B.2.8×10﹣4
C.﹣2.8×10﹣5 D.28×10﹣5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com