
����Ŀ��һ�п쳵�ɼؿ����ҵأ�һ���������ҵؿ����أ�����ͬʱ�����������˶����쳵���ҵص�·��y1��km������ʻ��ʱ��x��h��֮��ĺ�����ϵ����ͼ���߶�AB��ʾ���������ҵص�·��y2��km������ʻ��ʱ��x��h�� ֮��ĺ�����ϵ����ͼ���߶�OC��ʾ������ͼ���������̽������1���ס�������֮��ľ���Ϊ�� ��km����2���߶�AB�Ľ���ʽΪ�� �����߶�OC�Ľ���ʽΪ�� ������3����졢����֮��ľ���Ϊy��km������ֱ��д��y����ʻʱ��x��h���ĺ�����ϵʽ��

���𰸡���1��450km����2��![]() =��150x+450��0��x��3����OC�Ľ���ʽ��
=��150x+450��0��x��3����OC�Ľ���ʽ�� ![]() =75x��0��x��6��
=75x��0��x��6��
��3��y=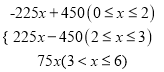 ��
��
�������������������1������A������Ϊ��0��450�������Եó��ף�������֮��ľ��룻��2������A������Ϊ��0��450����B������Ϊ��3��0��������y1=kx+b������ɣ������߶�OC����ʽΪy2=mx ���m���ɣ���3����y1=y2����150x+450=75x�����x=2���֢ٵ�0��x��2ʱ��y=y1��y2������2��x��3ʱ��y=y2��y1������3��x��6ʱ��y=y2�����������������ʽ����.
���ã�2��������ó���y=|y1-y2|���������������ʽ���ó�ͼ�ɣ�
���������
��1���ߵ�x=0ʱ��y1=450��
��ס�������֮��ľ���Ϊ450km��
�ʴ�Ϊ��450��
��2�����߶�AB�Ľ���ʽΪy1=kx+b���߶�OC�Ľ���ʽΪy2=mx��
����A��0��450����B��3��0������y1=kx+b��
![]() ����ã�
����ã�![]() ��
��
���߶�AB�Ľ���ʽΪy1=��150x+450��0��x��3����
����C��6��450������y2=mx��
6m=450����ã�m=75��
���߶�OC�Ľ���ʽΪy2=75x��0��x��6����
�ʴ�Ϊ��y1=��150x+450��0��x��3����y2=75x��0��x��6����
��3����y1=y2����150x+450=75x��
��ã�x=2��
��0��x��2ʱ��y=y1��y2=��150x+450��75x=��225x+450��
��2��x��3ʱ��y=y2��y1=75x������150x+450��=225x��450��
��3��x��6ʱ��y=y2=75x��
��졢����֮��ľ���y��km������ʻʱ��x��h���ĺ�����ϵʽΪy=![]() ��
��


 �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС�����½�50��ͣ��λ�����Խ��С��ͣ���ѵ�����.��֪�½�1������ͣ��λ��1������ͣ��λ����0.6��Ԫ���½�3������ͣ��λ��2������ͣ��λ����1.3��Ԫ.
��1����С���½�1������ͣ��λ��1������ͣ��λ���������Ԫ��
��2����С������ҵ����Ԥ��Ͷ�ʽ���12��Ԫ��������13��Ԫ����ô���м��ֽ���ͣ��λ�ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����㣺[��x��2y��2+��x��2y����x+2y����2x��2x��y��]��2x
��2���Ȼ�������ֵ��2b2+��a+b����a��b������a��b��2������a=��3��b=![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD��EF��AB��CD�ֱ��ཻ�ڵ�E��F��EP��EF�����EFD��ƽ����FP�ཻ�ڵ�P���ҡ�BEP=50�㣬���EPF=�� ���ȣ� 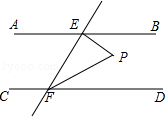
A.70
B.65
C.60
D.55
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������У���ʽ��ȷ����![]() ����
����![]()
A. �˽Ȿ����ѧ��ÿ��ѧϰ���õ�ʱ�䣬����ȫ�����ķ�ʽ
B. Ϊ��֤���ػ���ijɹ����䣬�������е��㲿�����ó�������ķ�ʽ
C. �˽�ij��ÿ��������˿���������ȫ�����ķ�ʽ
D. �˽�ȫ����ѧ����������������ó�������ķ�ʽ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���AΪx�Ḻ������һ�㣬��BΪx����������һ�㣬![]() ��
��![]() ������a��b�����ϵʽ��
������a��b�����ϵʽ��![]() ��
��
![]() ______��
______��![]() ______��
______��![]() �����Ϊ______��
�����Ϊ______��
![]() ��ͼ2��ʯ
��ͼ2��ʯ![]() �ڵ�C����P���߶�OC��һ�㣬����BP���ӳ�BP��AC�ڵ�
�ڵ�C����P���߶�OC��һ�㣬����BP���ӳ�BP��AC�ڵ�![]() ��
��![]() ʱ����֤��BPƽ��
ʱ����֤��BPƽ��![]() ��
��![]() ��ʾ�������������ڽǺ͵���
��ʾ�������������ڽǺ͵���![]()
![]() ��ͼ3����
��ͼ3����![]() ����E�ǵ�A���B֮����һ������CE����CBƽ��
����E�ǵ�A���B֮����һ������CE����CBƽ��![]() ��
��![]() ��
��![]() ��ʲô������ϵ����д������֮���������ϵ����˵�����ɣ�
��ʲô������ϵ����д������֮���������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�AB.
(1)��û�п̶ȵ�ֱ�ߺ�Բ�水������Ҫ����ͼ����C���߶�BA���ӳ���������CA��AB;
(2)��(1)�������AB��28 cm���߶�BC����һ��M�����߶�AM��BM��1��3�����߶�CM�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��Բ���ĵ���뾶��10 cm������18 cm�������Բ������ˮƽ�����ϣ���ͼ��ʾ��
(1)�����һ��ƽ����ˮƽ����ȥ�����Բ�������õĽ�����ʲô��״��
(2)�����һ��ƽ������ֱ����ȥ�����Բ�������õĽ�����ʲô��״��
(3)������ʱ���õĽ����dz������ҳ����ε����������㻭��������沢���������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ժũ���ƻ���ֲA��B���ֲ�ݮ��6Ķ�����ݱ�����Ϣ������������⣺
��Ŀ Ʒ�� | A | B |
��Ķ������λ��ǧ�ˣ� | 1200 | 2000 |
��ժ�۸� | 60 | 40 |
��1������ũ��ÿ���ݮȫ������ժ��������Ϊ460000Ԫ����ôA��B���ֲ�ݮ���ֶ���Ķ��
��2����Ҫ����ֲA�ֲ�ݮ��Ķ����������ֲB�ֲ�ݮ��һ�룬��ô��ֲA�ֲ�ݮ����Ķʱ����ʹ��ũ��ÿ���ݮȫ������ժ����������ࣿ�������������룮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com