
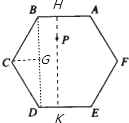
【题目】正六边形ABCDEF的边长为![]() cm,点P为ABCDEF内的任意一点,点P到正六边形ABCDEF各边所在直线的距离之和为s,则s=_____cm.
cm,点P为ABCDEF内的任意一点,点P到正六边形ABCDEF各边所在直线的距离之和为s,则s=_____cm.
【答案】18
【解析】过P作AB的垂线,交AB、DE分别为H、K,连接BD,由正六边形的性质可知AB∥DE,AF∥CD,BC∥EF,故HK⊥DE,过C作CG⊥BD,由等腰三角形的性质及正六边形的内角和定理可知,DB⊥AB⊥DE,再由锐角三角函数的定义可求出BG的长,进而可求出BD的长,由正六边形的性质可知点P到AF与CD的距离和及P到EF、BC的距离和均为BD的长,故可得出结论.
过P作AB的垂线,交AB、DE分别为H、K,连接BD,
∵六边形ABCDEF是正六边形,
∴AB∥DE,AF∥CD,BC∥EF,且P到AF与CD的距离和及P到EF、BC的距离和均为HK的长, ∵BC=CD,∠BCD=∠ABC=∠CDE=120°, ∴∠CBD=∠BDC=30°,
∴BD∥HK,且BD=HK, ∵CG⊥BD, ∴BD=2BG=2×BC×cos∠CBD=2×2![]() ×
×![]() =6,
=6,
∴点P到各边距离之和为3BD=3×6=18.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个可以自由转动的均匀转盘![]() ,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
①分别转动转盘![]() ;
;
②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停止在等份线上,那么重转一次,直到指针指向某一份为止).

【1】用列表法或树状图分别求出数字之积为3的倍数和数字之积为5的倍数的概率;
【2】小明和小亮想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小明得2分;数字之积为5的倍数时,小亮得3分.这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏对双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,已知直线
,已知直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() ,
,![]() 是直线
是直线![]() 上的一个动点.
上的一个动点.
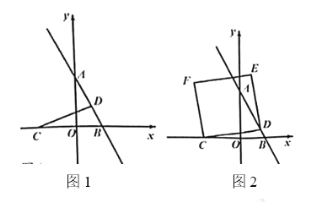
(1)求点![]() 的坐标,并求当
的坐标,并求当![]() 时点
时点![]() 的坐标;
的坐标;
(2)如图![]() ,以
,以![]() 为边在
为边在![]() 上方作正方形
上方作正方形![]() ,请画出当正方形
,请画出当正方形![]() 的另一顶点也落在直线
的另一顶点也落在直线![]() 上的图形,并求出此时
上的图形,并求出此时![]() 点的坐标;
点的坐标;
(3)当![]() 点在
点在![]() 上运动时,点
上运动时,点![]() 是否也在某个函数图象上运动?若是请直接写出该函数的解析式;若不在,请说明理由.
是否也在某个函数图象上运动?若是请直接写出该函数的解析式;若不在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在直线
在直线![]() 上,射线
上,射线![]() 在直线
在直线![]() 的上方,且
的上方,且![]()
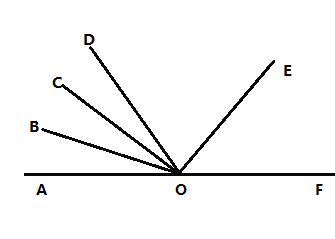
(1)如图1,![]() 在
在![]() 内部,且
内部,且![]() 平分
平分![]()
①若![]() =
=![]() ,则
,则![]() = .
= .
②若![]() =
=![]() ,则
,则![]() = .
= .
③若![]() =
=![]() ,则
,则![]() = °(用含
= °(用含![]() 的式子表示)
的式子表示)
(2)当![]() 在
在![]() 内部,且
内部,且![]() 平分
平分![]() 时,请画出图形;此时,
时,请画出图形;此时,![]() 与
与![]() 有怎样的数量关系?请说明理由.
有怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到永丰路的距离为100米的点P处.这时,一辆小轿车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒,![]() ,
,![]() .
.
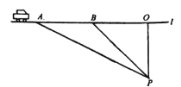
(1)求A、B之间的路程;
(2)请判断此车是否超过了永丰路每小时54千米的限制速度?(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列的解题过程,然后回答下列问题.
例:解绝对值方程:![]() .
.
解:讨论:①当![]() 时,原方程可化为
时,原方程可化为![]() ,它的解是
,它的解是![]() ;
;
②当![]() 时,原方程可化为
时,原方程可化为![]() ,它的解是
,它的解是![]() .
.
原方程的解为![]() 或
或![]() .
.
(1)依例题的解法,方程算![]() 的解是_______;
的解是_______;
(2)尝试解绝对值方程:![]() ;
;
(3)在理解绝对值方程解法的基础上,解方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.
(1)若∠MOE=27°,求∠AOC的度数;
(2)当∠BOD=x°(0<x<90)时,求∠MON的度数.
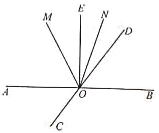
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com