
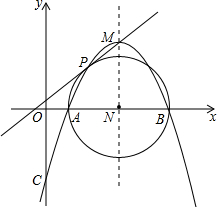
 如图,已知抛物线y=-$\frac{1}{2}$(x2-7x+6)的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
如图,已知抛物线y=-$\frac{1}{2}$(x2-7x+6)的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.分析 (1)利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,即可把一般式转化为顶点式,然后根据二次函数的性质求出抛物线的顶点坐标;
(2)连接BC,则BC与对称轴的交点为R,此时CR+AR的值最小;先求出点A、B、C的坐标,再利用待定系数法求出直线BC的解析式,进而求出其最小值和点R的坐标;
(3)设点P坐标为(x,-$\frac{1}{2}$x2+$\frac{7}{2}$x-3).根据NP=$\frac{1}{2}$AB=$\frac{5}{2}$列出方程(x-$\frac{7}{2}$)2+(-$\frac{1}{2}$x2+$\frac{7}{2}$x-3)2=($\frac{5}{2}$)2,解方程得到点P坐标,再计算得出PM2+PN2=MN2,根据勾股定理的逆定理得出∠MPN=90°,然后利用切线的判定定理即可证明直线MP是⊙N的切线.
解答 (1)解:∵y=-$\frac{1}{2}$(x2-7x+6)=-$\frac{1}{2}$(x2-7x)-3=-$\frac{1}{2}$(x-$\frac{7}{2}$)2+$\frac{25}{8}$,
∴抛物线的解析式化为顶点式为:y=-$\frac{1}{2}$(x-$\frac{7}{2}$)2+$\frac{25}{8}$,
顶点M的坐标是($\frac{7}{2}$,$\frac{25}{8}$);
(2)解:∵y=-$\frac{1}{2}$(x2-7x+6),
∴当y=0时,-$\frac{1}{2}$(x2-7x+6)=0,
解得x=1或6,
∴A(1,0),B(6,0),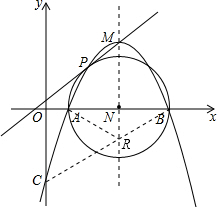 ∵x=0时,y=-3,
∵x=0时,y=-3,
∴C(0,-3).
连接BC,则BC与对称轴x=$\frac{7}{2}$的交点为R,连接AR,
则CR+AR=CR+BR=BC,根据两点之间线段最短可知此时CR+AR的值最小,
最小值为BC=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$.
设直线BC的解析式为y=kx+b,
∵B(6,0),C(0,-3),
∴$\left\{\begin{array}{l}{6k+b=0}\\{b=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-3}\end{array}\right.$,
∴直线BC的解析式为:y=$\frac{1}{2}$x-3,
令x=$\frac{7}{2}$,得y=$\frac{1}{2}$×$\frac{7}{2}$-3=-$\frac{5}{4}$,
∴R点坐标为($\frac{7}{2}$,-$\frac{5}{4}$);
(3)证明:设点P坐标为(x,-$\frac{1}{2}$x2+$\frac{7}{2}$x-3).
∵A(1,0),B(6,0),
∴N($\frac{7}{2}$,0),
∴以AB为直径的⊙N的半径为$\frac{1}{2}$AB=$\frac{5}{2}$,
∴NP=$\frac{5}{2}$,
即(x-$\frac{7}{2}$)2+(-$\frac{1}{2}$x2+$\frac{7}{2}$x-3)2=($\frac{5}{2}$)2,
化简整理得,x4-14x3+65x2-112x+60=0,
(x-1)(x-2)(x-5)(x-6)=0,
解得x1=1(与A重合,舍去),x2=2,x3=5(在对称轴的右侧,舍去),x4=6(与B重合,舍去),
∴点P坐标为(2,2).
∵M($\frac{7}{2}$,$\frac{25}{8}$),N($\frac{7}{2}$,0),
∴PM2=(2-$\frac{7}{2}$)2+(2-$\frac{25}{8}$)2=$\frac{225}{64}$,
PN2=(2-$\frac{7}{2}$)2+22=$\frac{25}{4}$=$\frac{400}{64}$,
MN2=($\frac{25}{8}$)2=$\frac{625}{64}$,
∴PM2+PN2=MN2,
∴∠MPN=90°,
∵点P在⊙N上,
∴直线MP是⊙N的切线.
点评 本题是二次函数的综合题,其中涉及到二次函数的图象与性质、待定系数法求一次函数的解析式、轴对称-最短路线问题以及切线的判定等知识,综合性较强,难度适中.第(3)问求出点P的坐标是解题的关键.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
| 甲种品牌化妆品 | 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 6 | 12 | 6 |
| 乙种品牌化妆品 | 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 12 | 6 | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com