
【题目】如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:

因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图1,当点Q在DC边上时,探究PB与PQ所满足的数量关系; 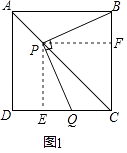
小明同学探究此问题的方法是:
过P点作PE⊥DC于E点,PF⊥BC于F点,
根据正方形的性质和角平分线的性质,得出PE=PF,
再证明△PEQ≌△PFB,可得出结论,他的结论应是
(2)如图2,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想. 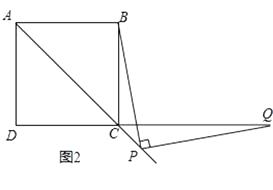
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要设计一幅长为3xcm、宽为2ycm的长方形图案,其中有两横两竖的彩条,横彩条的宽度为acm,竖彩条的宽度为bcm,问空白区域的面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”期间,某校部分团员准备购进一批“康乃馨”进行销售,并将所得利润捐给贫困同学的母亲.根据市场调查,这种“康乃馨”的销售量y(枝)与销售单价x(元/枝)之间成一次函数关系,它的部分图象如图. 
(1)试求y与x之间的函数关系式;
(2)若“康乃馨”的进价为5元/枝,且要求每枝的销售盈利不少于1元,问:在此次活动中,他们最多可购进多少数量的康乃馨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苹果的单价为a元/千克,香蕉的单价为b元/千克,买2千克苹果和3千克香蕉共需( )
A.(a+b)元
B.(3a+2b)元
C.(2a+3b)元
D.5(a+b)元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆DF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.

(1)若旗杆的高度FG是a米,用含a的代数式表示DG.
(2)小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上,![]() ,结果精确到0.1)
,结果精确到0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com