【题目】如图，在△ABC中，E点为AC的中点，其中BD=1，DC=3，BC= 
，AD= 
，求DE的长．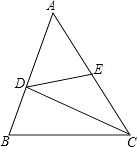 
【答案】解：∵BD=1，DC=3，BC= 
，
又∵12+32=（ ）2，
∴BD2+CD2=BC2，
∴△BCD是直角三角形且∠BDC=90°，
∴∠ADC=90°，
∴AC= 
=4，
又∵E点为AC的中点
∴DE= 
=2．
【解析】首先根据勾股定理的逆定理判定△BCD是直角三角形且∠BDC=90°，再利用勾股定理可求出AC的长，进而可求出DE的长．
【考点精析】关于本题考查的勾股定理的概念和勾股定理的逆定理，需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形才能得出正确答案．
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案科目：初中数学 来源： 题型：
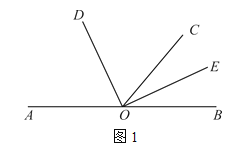
【题目】已知，O为直线AB上一点，∠DOE=90°．
（1）如图1，若∠AOC=130°，OD平分∠AOC．
①求∠BOD的度数；
②请通过计算说明OE是否平分∠BOC．
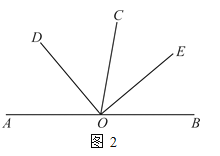
（2）如图2，若∠BOE：∠AOE=2：7，求∠AOD的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，BD垂直平分AC，垂足为点F，E为四边形ABCD外一点，且∠ADE=∠BAD，AE⊥AC． 
（1）求证：四边形ABDE是平行四边形；
（2）如果DA平分∠BDE，AB=5，AD=6，求AC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知四边形ABCD，对角线AC和BD相交于O，下面选项不能得出四边形ABCD是平行四边形的是（ ）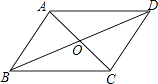 
A.AB∥CD，且AB=CD
B.AB=CD，AD=BC
C.AO=CO，BO=DO
D.AB∥CD，且AD=BC
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:
因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，请分别根据已知条件进行推理，得出结论，并在括号内注明理由．
①∵ ∠B=∠3(已知)，∴______∥______.(______，______)
②∵∠1=∠D (已知)，∴______∥______.(______，______)
③∵∠2=∠A (已知)，∴______∥______.(______，______)
④∵∠B+∠BCE=180° (已知)，∴______∥______.(______，______)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com