
【题目】我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据: ![]() ≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).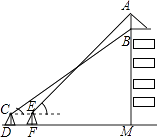
【答案】解:过点C作CN⊥AM于点N,则点C,E,N在同一直线上,
设AB=x米,则AN=x+(17﹣1)=x+16(米),
在Rt△AEN中,∠AEN=45°,
∴EN=AN=x+16,
在Rt△BCN中,∠BCN=37°,BM=17,
∴tan∠BCN= ![]() =0.75,
=0.75,
∴ ![]() =
= ![]() ,
,
解得:x=1 ![]() ≈1.3.
≈1.3.
经检验:x=1 ![]() 是原分式方程的解.
是原分式方程的解.
答:宣传牌AB的高度约为1.3m.
【解析】首先过点C作CN⊥AM于点N,则点C,E,N在同一直线上,设AB=x米,则AN=x+(17﹣1)=x+16(米),则在Rt△AEN中,∠AEN=45°,可得EN=AN=x+16,在Rt△BCN中,∠BCN=37°,BM=17,可得tan∠BCN= ![]() =0.75,则可得方程:
=0.75,则可得方程: ![]() ,解此方程即可求得答案.
,解此方程即可求得答案.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣4ax+3a(a>0),与y轴交于点A,在x轴的正半轴上取一点B,使OB=2OA,抛物线的对称轴与抛物线交于点C,与x轴交于点D,与直线AB交于点E,连接BC.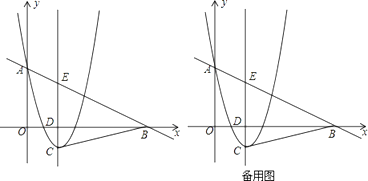
(1)求点B,C的坐标(用含a的代数式表示);
(2)若△BCD与△BDE相似,求a的值;
(3)连接OE,记△OBE的外心为M,点M到直线AB的距离记为h,请探究h的值是否会随着a的变化而变化?如果变化,请写出h的取值范围;如果不变,请求出h的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0),…,则点P2017的坐标是( )
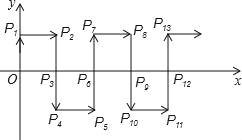
A. (671,﹣1) B. (672,0) C. (672,1) D. (672,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形。若![]() ,AB=2,则图中阴影部分的面积为( )
,AB=2,则图中阴影部分的面积为( )

A. 12-4![]() B. 5 C. 12-4
B. 5 C. 12-4![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON为锐角.下列说法:①∠MOP=![]() ∠MON;②∠MOP=∠NOP=
∠MON;②∠MOP=∠NOP=![]() ∠MON;③∠MOP=∠NOP;④∠MON=∠MOP+∠NOP.其中,能说明射线OP一定为∠MON的平分线的有( )
∠MON;③∠MOP=∠NOP;④∠MON=∠MOP+∠NOP.其中,能说明射线OP一定为∠MON的平分线的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,如果直线l上依次有3个点A、B、C,那么
![]()
(1)在直线l上共有多少射线?多少条线段?
(2)在直线l上增加一个点,共增加了多少条射线?多少条线段?
(3)如果在直线l上增加到n个点,则共有多少条射线?多少条线段?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为( ) 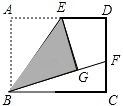
A.3 ![]()
B.2 ![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.
获奖等级 | 频数 |
一等奖 | a |
二等奖 | b |
三等奖 | 275 |

(1)表格中a的值为 , b的值为 .
(2)扇形统计图中表示获得一等奖的扇形的圆心角为度.
(3)估计全市有多少名学生获得三等奖?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com