
【题目】如图,抛物线y=ax2﹣4ax+3a(a>0),与y轴交于点A,在x轴的正半轴上取一点B,使OB=2OA,抛物线的对称轴与抛物线交于点C,与x轴交于点D,与直线AB交于点E,连接BC.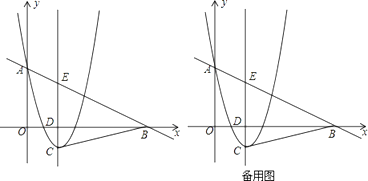
(1)求点B,C的坐标(用含a的代数式表示);
(2)若△BCD与△BDE相似,求a的值;
(3)连接OE,记△OBE的外心为M,点M到直线AB的距离记为h,请探究h的值是否会随着a的变化而变化?如果变化,请写出h的取值范围;如果不变,请求出h的值.
【答案】
(1)
解:由抛物线的解析式可知:点C的坐标为(2,﹣a),
令x=0代入y=ax2﹣4ax+3a,
∴y=3a,
∴OA=3a,
∵OB=2OA=6a,
∴点B的坐标为(6a,0)
(2)
解:由(1)可知:OD=2,CD=a,OB=6a,
若点B在点D的右侧时,如图1,
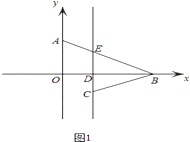
则6a>2,
∴a> ![]() ,
,
∴BD=6a﹣2,
当∠DBC=∠EBD时,
∴tan∠DBC=tan∠EBD= ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴a= ![]() ,
,
当∠DCB=∠EBD时,
∴tan∠DCB=tan∠EBD= ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴a= ![]() ,
,
若点B在点D的左侧时,如图2,
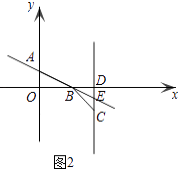
则0<6a<2,
∴0<a< ![]() ,
,
∴BD=2﹣6a,
当∠DBC=∠EBD时,
∴tan∠DBC=tan∠EBD= ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴a= ![]() ,
,
当∠DCB=∠EBD时,
∴tan∠DCB=tan∠EBD= ![]() ,
,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴a= ![]() ,
,
若点B与点D重合时,
则6a=2,
∴a= ![]() ,
,
此情况不存在△BCD与△BDE,
综上所述,a的值为 ![]() 、
、 ![]() 、
、 ![]() 和
和 ![]()
(3)
解:由题意知:点M在OB和BE的垂直平分线上,
设OB和BE的垂直平分线交于点M,
其中OB的垂直平分线与OB交于点G,
BE的垂直平分线交OB于点H,交BE于点F
当点B在点D的右侧时,如图3,
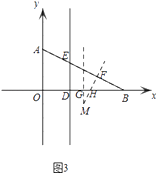
∴6a>2,
∴a> ![]() ,
,
∴BD=6a﹣2,
∵tan∠EBD= ![]() ,
,
∴ED= ![]() BD=3a﹣1,
BD=3a﹣1,
由勾股定理可求得:BE=3 ![]() a﹣
a﹣ ![]() ,
,
∴BF= ![]() BE=
BE= ![]() ,
,
∴HF= ![]() BF=
BF= ![]() ,
,
∴由勾股定理可求得:BH= ![]() ,
,
∴HG=BG﹣BH= ![]() ,
,
∵∠GMH=∠EBD,
∴sin∠GMH=sin∠EBD= ![]() ,
,
∴MH= ![]() HG=
HG= ![]() ,
,
∴MF=MH+HF= ![]() ,
,
当点B在点D的左侧时,如图:
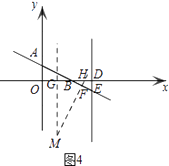
∴0<a< ![]() ,
,
∴BD=OD﹣OB=2﹣6a,
∵tan∠ABO=tan∠DBE= ![]() ,
,
∴DE= ![]() BD=1﹣3a,
BD=1﹣3a,
∴由勾股定理可求得:BE= ![]() ﹣3
﹣3 ![]() a,
a,
∴BF= ![]() BE=
BE= ![]() ,
,
∴HF= ![]() BF=
BF= ![]() ,
,
由勾股定理求得:BH= ![]() ,
,
∵GB= ![]() OB=3a,
OB=3a,
∴GH=GB+BH= ![]() ,
,
∵∠HBF+∠BHF=90°,
∠GMH+∠BHF=90°,
∴∠HBF=∠GMH,
∴sin∠HBF=sin∠GMH= ![]() ,
,
∴MH= ![]() GH=
GH= ![]() ,
,
∴MF=MH﹣HF= ![]() ,
,
当点B与点D重合时,
此时a= ![]() ,
,
此情况不符合题意,舍去
综上所述,点M到直线AB的距离不会变化,始终为 ![]() .
.
【解析】(1)令x=0代入抛物线可得y=3a,即OA=3a,因为OB=2OA,所以B的坐标为(6a,0),点C时抛物线的顶点,利用顶点坐标公式即可求出C的坐标为(2,﹣a);(2)由于点B的位置不确定,所以分三种情况讨论,一是点B在点D的左侧,二是点B在点D的右侧,三是点B与点D重合,其中第三种情况是不存在△BCD与△BDE;另外,△BCD与△BDE相似时,有两种情况,一是∠DBC=∠EBD,二是∠DBE=∠DBC,利用相似三角形的性质即可求出a的值;(3)由于点B的位置不确定,所以分三种情况讨论,一是点B在点D的左侧,二是点B在点D的右侧,三是点B与点D重合,其中第三种情况是不存在△OBE,由题意知:点M在OB和BE的垂直平分线上,设OB和BE的垂直平分线交于点M,其中OB的垂直平分线与OB交于点G,BE的垂直平分线交OB于点H,交BE于点F,利用相似三角形的性质求出MF的长度即可;


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
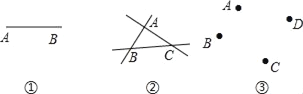
【题目】观察图①,由点A和点B可确定 条直线;
观察图②,由不在同一直线上的三点A、B和C最多能确定 条直线;
(1)动手画一画图③中经过A、B、C、D四点的所有直线,最多共可作 条直线;
(2)在同一平面内任三点不在同一直线的五个点最多能确定 条直线、n个点(n≥2)最多能确定 条直线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.

(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了满足学生借阅图书的需求,计划购买一批新书.为此,该校图书管理员对一周内本校学生从图书馆借出各类图书的数量进行了统计,结果如下图.

请你根据统计图中的信息,解答下列问题:
(1)补全条形图和扇形图;
(2)该校学生最喜欢借阅哪类图书?
(3)该校计划购买新书共600本,若按扇形统计图中的百分比来相应地确定漫画、科普、文学、其它这四类图书的购买量,求应购买这四类图书各多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人共收集邮票若干张,其中![]() 是2000年以前的国内外发行的邮票,
是2000年以前的国内外发行的邮票,![]() 是2001年国内发行的,
是2001年国内发行的,![]() 是2002年国内发行的,此外尚有不足100张的国外邮票.求该人共有多少张邮票.
是2002年国内发行的,此外尚有不足100张的国外邮票.求该人共有多少张邮票.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知反比例函数y=![]() 的图象与一次函数y=ax+b的图象交于M(2,m)和N(-1,-4)两点.
的图象与一次函数y=ax+b的图象交于M(2,m)和N(-1,-4)两点.
(1)求这两个函数的解析式;
(2)求△MON的面积;
(3)请判断点P(4,1)是否在这个反比例函数的图象上,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,对任意一个正整数n都可以进行这样的分解:n=p![]() q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p
q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p![]() q是n的最佳分解,并规定:F(n)=
q是n的最佳分解,并规定:F(n)=![]() ,例如12可以分解为1
,例如12可以分解为1![]() 12,2
12,2![]() 6或3
6或3![]() 4,因为12-1>6-2>4-3,所以3
4,因为12-1>6-2>4-3,所以3![]() 4是最佳分解,所以F(n)=
4是最佳分解,所以F(n)=![]() 。
。
(1)如果一个正整数![]() 是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1
是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1
(2)如果一个两位正整数t,t=10x+y (1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们就称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据: ![]() ≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).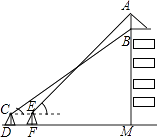
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com