
【题目】我们知道,对任意一个正整数n都可以进行这样的分解:n=p![]() q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p
q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p![]() q是n的最佳分解,并规定:F(n)=
q是n的最佳分解,并规定:F(n)=![]() ,例如12可以分解为1
,例如12可以分解为1![]() 12,2
12,2![]() 6或3
6或3![]() 4,因为12-1>6-2>4-3,所以3
4,因为12-1>6-2>4-3,所以3![]() 4是最佳分解,所以F(n)=
4是最佳分解,所以F(n)=![]() 。
。
(1)如果一个正整数![]() 是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1
是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1
(2)如果一个两位正整数t,t=10x+y (1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们就称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值。
【答案】(1)见解析;(2)F(t)的最大值为![]()
【解析】试题分析:(1)根据题意可设![]() 由最佳分解定义可得
由最佳分解定义可得![]()
(2)根据“吉祥数”定义知(10y+x)(10x+y)=9(yx)=18,即y=x+2,结合![]() 的范围可得2位数的“吉祥数”,求出每个“吉祥数”
的范围可得2位数的“吉祥数”,求出每个“吉祥数”![]() 的值.即可求出最大值.
的值.即可求出最大值.
试题解析:(1)对任意一个完全平方数m,设![]() (n为正整数),
(n为正整数),
∵|nn|=0,
∴n×n是m的最佳分解,
∴对任意一个完全平方数m, ![]()
(2)设交换t的个位上的数与十位上的数得到的新数为t′,则t′=10y+x,
∵t为“吉祥数”,
∴t′t=(10y+x)(10x+y)=9(yx)=18,
∴y=x+2,
∵![]() x,y为自然数,
x,y为自然数,
∴“吉祥数”有:13,24,35,46,57,68,79,
∴所有“吉祥数”中F(t)的值为: ![]()
![]() 的最大值为
的最大值为![]()


科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AD是⊙O的直径,EA是⊙O的切线.若∠EAC=120°,则∠ABC的度数是( ) 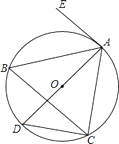
A.80°
B.70°
C.60°
D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣4ax+3a(a>0),与y轴交于点A,在x轴的正半轴上取一点B,使OB=2OA,抛物线的对称轴与抛物线交于点C,与x轴交于点D,与直线AB交于点E,连接BC.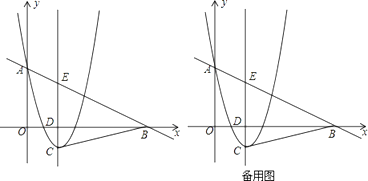
(1)求点B,C的坐标(用含a的代数式表示);
(2)若△BCD与△BDE相似,求a的值;
(3)连接OE,记△OBE的外心为M,点M到直线AB的距离记为h,请探究h的值是否会随着a的变化而变化?如果变化,请写出h的取值范围;如果不变,请求出h的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进A.B两种商品共160件,其进价和售价如表:
A | B | |
进价(元/件) | 15 | 35 |
售价(元/件) | 20 | 45 |
(1)当A.B两种商品分别购进多少件时,商店计划售完这批商品后能获利1100元;
(2)若商店计划购进A种商品不少于66件,且销售完这批商品后获利多于1260元,请你帮该商店老板预算有几种购货方案?获利最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣(x﹣1)2+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,CD∥x轴交抛物线另一点D,连结AC,DE∥AC交边CB于点E. 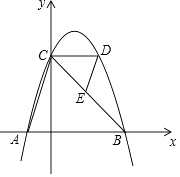
(1)求A,B两点的坐标;
(2)求△CDE与△BAC的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠C=90°,AC=BC= ![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ) 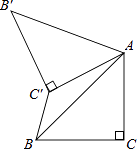
A.2﹣ ![]()
B.![]()
C.![]() ﹣1
﹣1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0),…,则点P2017的坐标是( )
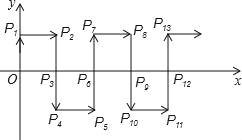
A. (671,﹣1) B. (672,0) C. (672,1) D. (672,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为( ) 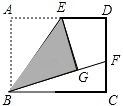
A.3 ![]()
B.2 ![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com