
【题目】如图,已知△ABC中,∠C=90°,AC=BC= ![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ) 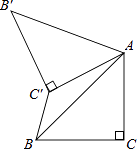
A.2﹣ ![]()
B.![]()
C.![]() ﹣1
﹣1
D.1
【答案】C
【解析】解:如图,连接BB′, ∵△ABC绕点A顺时针方向旋转60°得到△AB′C′,
∴AB=AB′,∠BAB′=60°,
∴△ABB′是等边三角形,
∴AB=BB′,
在△ABC′和△B′BC′中,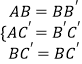 ,
,
∴△ABC′≌△B′BC′(SSS),
∴∠ABC′=∠B′BC′,
延长BC′交AB′于D,
则BD⊥AB′,
∵∠C=90°,AC=BC= ![]() ,
,
∴AB= ![]() =2,
=2,
∴BD=2× ![]() =
= ![]() ,
,
C′D= ![]() ×2=1,
×2=1,
∴BC′=BD﹣C′D= ![]() ﹣1.
﹣1.
故选:C.
【考点精析】认真审题,首先需要了解旋转的性质(①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了).


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
【题目】已知两直线L1:y=k1x+b1,L2:y=k2x+b2,若L1⊥L2,则有k1k2=﹣1.
(1)应用:已知y=2x+1与y=kx﹣1垂直,求k;
(2)直线经过A(2,3),且与y=![]() x+3垂直,求解析式.
x+3垂直,求解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
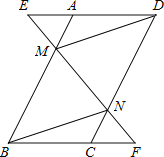
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,对任意一个正整数n都可以进行这样的分解:n=p![]() q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p
q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p![]() q是n的最佳分解,并规定:F(n)=
q是n的最佳分解,并规定:F(n)=![]() ,例如12可以分解为1
,例如12可以分解为1![]() 12,2
12,2![]() 6或3
6或3![]() 4,因为12-1>6-2>4-3,所以3
4,因为12-1>6-2>4-3,所以3![]() 4是最佳分解,所以F(n)=
4是最佳分解,所以F(n)=![]() 。
。
(1)如果一个正整数![]() 是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1
是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1
(2)如果一个两位正整数t,t=10x+y (1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们就称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
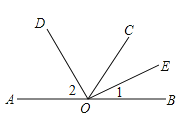
【题目】如图,O是直线AB上的一点,C是直线AB外的一点,OD是∠AOC的平分线,
OE是∠COB的平分线.
(1)已知∠1=23°,求∠2的度数;
(2)无论点C的位置如何改变,图中是否存在一个角,它的大小始终不变(∠AOB除外)?如果存在,求出这个角的度数;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合并下列多项式中的同类项:
(1)3x2+4x﹣2x2﹣x+x2﹣3x﹣1;
(2)﹣a2b+2a2b;
(3)a3﹣a2b+ab2+a2b﹣2ab2+b3;
(4)2a2b+3a2b﹣![]() a2b
a2b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三角形ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).
(1)三角形A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标.
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是( )
①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.

A. ①② B. ①④ C. ①③④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com