
【题目】已知,如图,在ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
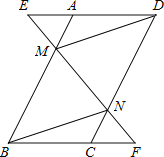
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
【答案】见解析
【解析】
试题分析:(1)先根据平行四边形的性质可得出AD∥BC,∠DAB=∠BCD,再根据平行线的性质及补角的性质得出∠E=∠F,∠EAM=∠FCN,从而利用ASA可作出证明;
(2)根据平行四边形的性质及(1)的结论可得BM![]() DN,则由有一组对边平行且相等的四边形是平行四边形即可证明.
DN,则由有一组对边平行且相等的四边形是平行四边形即可证明.
证明:(1)四边形ABCD是平行四边形,
∴∠DAB=∠BCD,
∴∠EAM=∠FCN,
又∵AD∥BC,
∴∠E=∠F.
∵在△AEM与△CFN中,
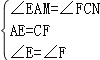 ,
,
∴△AEM≌△CFN(ASA);
(2)∵四边形ABCD是平行四边形,
∴AB![]() CD,
CD,
又由(1)得AM=CN,
∴BM![]() DN,
DN,
∴四边形BMDN是平行四边形.


科目:初中数学 来源: 题型:
【题目】一个不透明的袋中,装有10个红球、2个黄球、8个篮球,它们除颜色外都相同.
(1)求从袋中摸出一个球是红球的概率;
(2)现从袋中取出若干个红球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率是 ![]() ,问取出了多少个红球?
,问取出了多少个红球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进A.B两种商品共160件,其进价和售价如表:
A | B | |
进价(元/件) | 15 | 35 |
售价(元/件) | 20 | 45 |
(1)当A.B两种商品分别购进多少件时,商店计划售完这批商品后能获利1100元;
(2)若商店计划购进A种商品不少于66件,且销售完这批商品后获利多于1260元,请你帮该商店老板预算有几种购货方案?获利最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B的坐标分别为(0,8),(﹣3,0),点P从点A出发,以2单位/秒的速度沿射线AO方向运动,同时点E从点B出发,以1单位/秒的速度沿射线BO方向运动,以PE为斜边构造Rt△PEC(字母按逆时针顺序),且EC=2PC,抛物线y=﹣2x2+bx+c经过点(0,4),(﹣1,﹣2),设运动时间为t秒.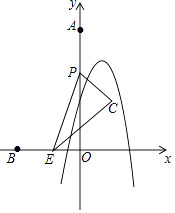
(1)求该抛物线的表达式;
(2)当t=2时,求点C的坐标;
(3)①当t<3时,求点C的坐标(用含t的代数式表示);
②在运动过程中,若点C恰好落在该抛物线上,请直接写出所有满足条件的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠C=90°,AC=BC= ![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ) 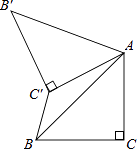
A.2﹣ ![]()
B.![]()
C.![]() ﹣1
﹣1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,且∠ABC=60°,AB=BC,△ACD的外接圆⊙O交BC于E点,连接DE并延长,交AC于P点,交AB延长线于F. 
(1)求证:CF=DB;
(2)当AD= ![]() 时,试求E点到CF的距离.
时,试求E点到CF的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ![]() ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
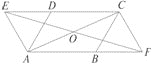
(1)求证:四边形AFCE是平行四边形.
(2)若去掉已知条件的“∠DAB=60°,上述的结论还成立吗 ”若成立,请写出证明过程;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com