
����Ŀ����ͼ����A��B������ֱ�Ϊ��0��8��������3��0������P�ӵ�A��������2��λ/����ٶ�������AO�����˶���ͬʱ��E�ӵ�B��������1��λ/����ٶ�������BO�����˶�����PEΪб�߹���Rt��PEC����ĸ����ʱ��˳����EC=2PC��������y=��2x2+bx+c�����㣨0��4��������1����2�������˶�ʱ��Ϊt�룮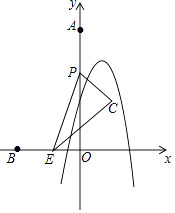
��1����������ߵı���ʽ��
��2����t=2ʱ�����C�����ꣻ
��3���ٵ�t��3ʱ�����C�����꣨�ú�t�Ĵ���ʽ��ʾ����
�����˶������У�����Cǡ�����ڸ��������ϣ���ֱ��д����������������t��ֵ��
���𰸡�
��1��
�⣺��������y=��2x2+bx+c�����㣨0��4��������1����2����
�� ![]()
�� ![]() ��
��
�������ߵĽ���ʽΪy=��2x2+4x+4��
��2��
�⣺��ͼ1�У�t=2ʱ��EO=1��OP=4����C��x��y������CH��x����H��PQ��HC��Q��

�ߡ�PCQ+��CPQ=90�㣬��ECH+��PCQ=90�㣬
���CPQ=��ECH���ߡ�Q=��CHE=90�㣬
���PCQ�ס�CEH��
�� ![]()
��EC=2PC��
�� ![]() =
= ![]() =
= ![]() ��
��
��x= ![]() ��y=
��y= ![]() ��
��
���C���꣨ ![]() ��
�� ![]() ��
��
��3��
�⣺����ͼ1�У���C��x��y������PO=8��2t��EH=3��t+x��CH=y��QC=8��2t��y��PQ=x��
�ߡ�PCQ�ס�CEH��
�� ![]()
��EC=2PC��
�� ![]() =
= ![]() =
= ![]() ��
��
��x= ![]() ��y=
��y= ![]() ��
��
���C���꣨ ![]() ��
�� ![]() ����
����
�ڵ�t��3ʱ�������C���������ϣ����� ![]() =��2��
=��2�� ![]() ��2+4
��2+4 ![]() +4��
+4��
���t=1��6����������
��t=1ʱ����C���������ϣ�
��3��t��4ʱ����ͼ���֪�������������ĵ�C���������ϣ�
��t��4ʱ����ͼ2�У���CH��x����H��PQ��HC��Q��

��C��x��y������PO=2t��8��EH=t��3��x��CH=��y��QC=2t��8+y��PQ=��x��
�ߡ�PCQ�ס�CEH��
�� ![]()
��EC=2PC��
�� ![]() =
= ![]() =
= ![]() ��
��
��x= ![]() ��y=
��y= ![]() ��
��
���C���꣨ ![]() ��
�� ![]() ����
����
�����C���������ϣ����� ![]() =��2��
=��2�� ![]() ��2+4
��2+4 ![]() +4��
+4��
���t=6��1����������
��t=6ʱ����C���������ϣ�
��������t=1��6sʱ����C ��������
����������1���ѣ�0��4��������1����2�����������߽���ʽy=��2x2+bx+c���з����鼴�ɽ�����⣮��2����ͼ1�У�t=2ʱ��EO=1��OP=4����C��x��y������CH��x����H��PQ��HC��Q���ɡ�PCQ�ס�CEH���� ![]() =
= ![]() =
= ![]() ���г������飬�ⷽ���鼴�ɽ�����⣮��3������ͼ1�У���C��x��y������PO=8��2t��EH=3��t+x��CH=y��QC=8��2t��y��PQ=x���ɡ�PCQ�ס�CEH����
���г������飬�ⷽ���鼴�ɽ�����⣮��3������ͼ1�У���C��x��y������PO=8��2t��EH=3��t+x��CH=y��QC=8��2t��y��PQ=x���ɡ�PCQ�ס�CEH���� ![]() =
= ![]() =
= ![]() ����EC=2PC���ɵ�
����EC=2PC���ɵ� ![]() =
= ![]() =
= ![]() ����t��ʾx��y���ɽ�����⣮�ڷ���������t��3ʱ���г����̼��ɽ�����⣮��3��t��4ʱ����Ȼ�����������ĵ�C���������ϣ���t��4ʱ����ͼ2�У���CH��x����H��PQ��HC��Q����C��x��y������PO=2t��8��EH=t��3��x��CH=��y��QC=2t��8+y��PQ=��x���ɡ�PCQ�ס�CEH���õ�
����t��ʾx��y���ɽ�����⣮�ڷ���������t��3ʱ���г����̼��ɽ�����⣮��3��t��4ʱ����Ȼ�����������ĵ�C���������ϣ���t��4ʱ����ͼ2�У���CH��x����H��PQ��HC��Q����C��x��y������PO=2t��8��EH=t��3��x��CH=��y��QC=2t��8+y��PQ=��x���ɡ�PCQ�ס�CEH���õ� ![]() =
= ![]() =
= ![]() ���ⷽ���鼴�ɵõ���C���꣬�����������ɽ�����⣮
���ⷽ���鼴�ɵõ���C���꣬�����������ɽ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���ADC��ƽ���߽�AB�ڵ�E����ABC��ƽ���߽�CD�ڵ�F����֤���ı���EBFD��ƽ���ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǡ�ABC�����Բ������A����O��������ֱ��CD���ӳ��߽��ڵ�E����֪AE=AC�� 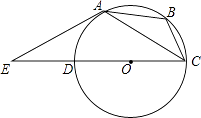
��1�����B�Ķ�����
��2����ED=1����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
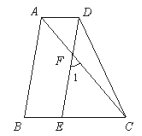
����Ŀ����ͼ,AB��DE,��1=��ACB��ACƽ�֡�BAD��
(1)��˵��: AD��BC��
(2)����B=80�������ADE�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABCD�У��ӳ�DA����E���ӳ�BC����F��ʹ��AE=CF������EF���ֱ�AB��CD�ڵ�M��N������DM��BN��
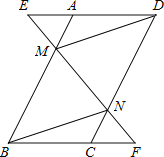
��1����֤����AEM�ա�CFN��
��2����֤���ı���BMDN��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����CΪ�߶�AD��һ�㣬BΪCD���е㣬��AD=10cm��BD=4cm��
��1��ͼ�й��ж������߶Σ�д����Щ�߶Σ�
��2����AC�ij���
��3������E��ֱ��AD�ϣ���AE=3cm����BE�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
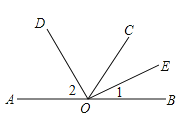
����Ŀ����ͼ��O��ֱ��AB�ϵ�һ�㣬C��ֱ��AB���һ�㣬OD�ǡ�AOC��ƽ���ߣ�
OE�ǡ�COB��ƽ���ߣ�
��1����֪��1=23�������2�Ķ�����
��2�����۵�C��λ����θı䣬ͼ���Ƿ����һ���ǣ����Ĵ�Сʼ�ղ��䣨��AOB���⣩��������ڣ��������ǵĶ�������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y= ![]() x2+bx+c��ͼ����x�ύ��A��3��0����B����1��0������y�ύ�ڵ�C������P��Qͬʱ��A�����������ÿ��1����λ���ȵ��ٶȷֱ���AB��AC���˶�������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶���
x2+bx+c��ͼ����x�ύ��A��3��0����B����1��0������y�ύ�ڵ�C������P��Qͬʱ��A�����������ÿ��1����λ���ȵ��ٶȷֱ���AB��AC���˶�������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶���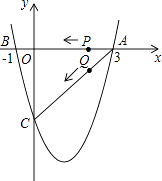
��1����ö��κ����Ľ���ʽ����C�����ꣻ
��2������P�˶���B��ʱ����Qֹͣ�˶�����ʱ����x�����Ƿ���ڵ�E��ʹ����A��E��QΪ�����������Ϊ���������Σ������ڣ������E�����ꣻ�������ڣ���˵�����ɣ�
��3����P��Q�˶���t��ʱ����APQ��PQ���ۣ���Aǡ��������������D�㴦�����ж���ʱ�ı���APDQ����״�������D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���뾶Ϊ1cm��Բ�Ľ�Ϊ90�������OAB�У��ֱ���OA��OBΪֱ������Բ����ͼ����Ӱ���ֵ����Ϊ�� �� 
A.��cm2
B.![]() ��cm2
��cm2
C.![]() cm2
cm2
D.![]() cm2
cm2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com