
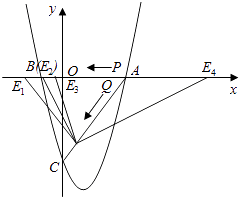
【题目】如图,二次函数y= ![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.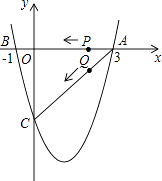
(1)求该二次函数的解析式及点C的坐标;
(2)当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E,使得以A,E,Q为顶点的三角形为等腰三角形?若存在,请求出E点坐标;若不存在,请说明理由.
(3)当P,Q运动到t秒时,△APQ沿PQ翻折,点A恰好落在抛物线上D点处,请判定此时四边形APDQ的形状,并求出D点坐标.
【答案】
(1)
解:∵二次函数y= ![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),
∴ 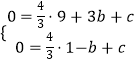 ,
,
解得 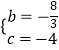 ,
,
∴y= ![]() x2﹣
x2﹣ ![]() x﹣4.
x﹣4.
∴C(0,﹣4)
(2)
解:方法(1):存在.
如图1,过点Q作QD⊥OA于D,此时QD∥OC,
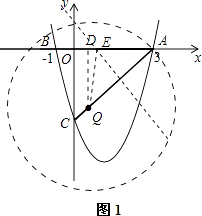
∵A(3,0),B(﹣1,0),C(0,﹣4),O(0,0),
∴AB=4,OA=3,OC=4,
∴AC= ![]() =5,
=5,
∵当点P运动到B点时,点Q停止运动,AB=4,
∴AQ=4.
∵QD∥OC,
∴ ![]() ,
,
∴ ![]() ,
,
∴QD= ![]() ,AD=
,AD= ![]() .
.
①作AQ的垂直平分线,交AO于E,此时AE=EQ,即△AEQ为等腰三角形,
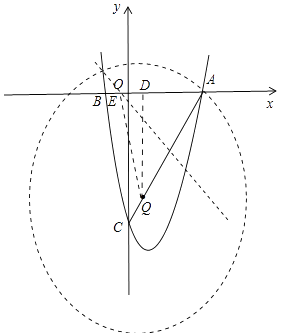
设AE=x,则EQ=x,DE=AD﹣AE=| ![]() ﹣x|,
﹣x|,
∴在Rt△EDQ中,( ![]() ﹣x)2+(
﹣x)2+( ![]() )2=x2,解得 x=
)2=x2,解得 x= ![]() ,
,
∴OA﹣AE=3﹣ ![]() =﹣
=﹣ ![]() ,
,
∴E(﹣ ![]() ,0),
,0),
说明点E在x轴的负半轴上;
②以Q为圆心,AQ长半径画圆,交x轴于E,此时QE=QA=4,
∵ED=AD= ![]() ,
,
∴AE= ![]() ,
,
∴OA﹣AE=3﹣ ![]() =﹣
=﹣ ![]() ,
,
∴E(﹣ ![]() ,0).
,0).
③当AE=AQ=4时,
(i).当E在A点左边时,
∵OA﹣AE=3﹣4=﹣1,
∴E(﹣1,0).
(ii).当E在A点右边时,
∵OA+AE=3+4=7,
∴E(7,0).
综上所述,存在满足条件的点E,点E的坐标为(﹣ ![]() ,0)或(﹣
,0)或(﹣ ![]() ,0)或(﹣1,0)或(7,0)
,0)或(﹣1,0)或(7,0)
方法二:
∵点P、Q同时从A点出发,都已每秒1个单位长度的速度分别沿AB,AC运动.过点Q作x轴垂线,垂足为H.
∵A(3,0),C(0,4),
∴lAC:y= ![]() x﹣4,
x﹣4,
∵点P运动到B点时,点Q停止运动,
∴AP=AQ=4,
∴QH= ![]() ,Qy=﹣
,Qy=﹣ ![]() ,
,
代入LAC:y= ![]() x﹣4得,Qx=
x﹣4得,Qx= ![]() ,则Q(
,则Q( ![]() ,﹣
,﹣ ![]() ),
),
∵点E在x轴上,
∴设E(a,0),
∵A(3,0),Q( ![]() ,﹣
,﹣ ![]() ),△AEQ为等腰三角形,
),△AEQ为等腰三角形,
∴AE=EQ,AE=AQ,EQ=AQ,
∴(a﹣3)2=(a﹣ ![]() )2+(0+
)2+(0+ ![]() )2,∴a=﹣
)2,∴a=﹣ ![]() ,
,
(a﹣3)2=(3﹣ ![]() )2+(0+
)2+(0+ ![]() )2,∴a1=7,a2=﹣1,
)2,∴a1=7,a2=﹣1,
(a﹣ ![]() )2+(0+
)2+(0+ ![]() )2=(3﹣
)2=(3﹣ ![]() )2+(0+
)2+(0+ ![]() )2,∴a1=﹣
)2,∴a1=﹣ ![]() ,a2=3(舍)
,a2=3(舍)
∴点E的坐标为(﹣ ![]() ,0)或(﹣
,0)或(﹣ ![]() ,0)或(﹣1,0)或(7,0)
,0)或(﹣1,0)或(7,0)
(3)
解:方法(1):四边形APDQ为菱形,D点坐标为(﹣ ![]() ,﹣
,﹣ ![]() ).理由如下:
).理由如下:
如图2,D点关于PQ与A点对称,过点Q作,FQ⊥AP于F,
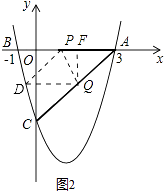
∵AP=AQ=t,AP=DP,AQ=DQ,
∴AP=AQ=QD=DP,
∴四边形AQDP为菱形,
∵FQ∥OC,
∴ ![]() ,
,
∴ ![]() ,
,
∴AF= ![]() ,FQ=
,FQ= ![]() ,
,
∴Q(3﹣ ![]() ,﹣
,﹣ ![]() ),
),
∵DQ=AP=t,
∴D(3﹣ ![]() ﹣t,﹣
﹣t,﹣ ![]() ),
),
∵D在二次函数y= ![]() x2﹣
x2﹣ ![]() x﹣4上,
x﹣4上,
∴﹣ ![]() =
= ![]() (3﹣
(3﹣ ![]() t)2﹣
t)2﹣ ![]() (3﹣
(3﹣ ![]() t)﹣4,
t)﹣4,
∴t= ![]() ,或t=0(与A重合,舍去),
,或t=0(与A重合,舍去),
∴D(﹣ ![]() ,﹣
,﹣ ![]() )
)
方法二:
∵P,Q运动到t秒,
∴设P(3﹣t,0),Q(3﹣ ![]() t,﹣
t,﹣ ![]() t),
t),
∴KPQ= 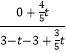 ,KPQ=﹣2,
,KPQ=﹣2,
∵AD⊥PQ,
∴KPQKAD=﹣1,
∴KAD= ![]() span> ,
span> ,
∵A(3,0),
∴lAD:y= ![]() x﹣
x﹣ ![]() ,
,
∵y= ![]() ,
,
∴x1=3(舍),x2=﹣ ![]() ,
,
∴D(﹣ ![]() ,﹣
,﹣ ![]() ),
),
∵DY=QY,即﹣ ![]() t=﹣
t=﹣ ![]() ,t=
,t= ![]() ,DQ∥AP,DQ=AQ=AP,此时四边形APDQ的形状为菱形.
,DQ∥AP,DQ=AQ=AP,此时四边形APDQ的形状为菱形.
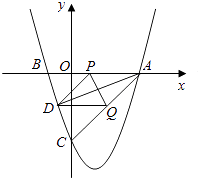
【解析】(1)将A,B点坐标代入函数y= ![]() x2+bx+c中,求得b、c,进而可求解析式及C坐标.(2)等腰三角形有三种情况,AE=EQ,AQ=EQ,AE=AQ.借助垂直平分线,画圆易得E大致位置,设边长为x,表示其他边后利用勾股定理易得E坐标.(3)注意到P,Q运动速度相同,则△APQ运动时都为等腰三角形,又由A、D对称,则AP=DP,AQ=DQ,易得四边形四边都相等,即菱形.利用菱形对边平行且相等等性质可用t表示D点坐标,又D在E函数上,所以代入即可求t,进而D可表示.
x2+bx+c中,求得b、c,进而可求解析式及C坐标.(2)等腰三角形有三种情况,AE=EQ,AQ=EQ,AE=AQ.借助垂直平分线,画圆易得E大致位置,设边长为x,表示其他边后利用勾股定理易得E坐标.(3)注意到P,Q运动速度相同,则△APQ运动时都为等腰三角形,又由A、D对称,则AP=DP,AQ=DQ,易得四边形四边都相等,即菱形.利用菱形对边平行且相等等性质可用t表示D点坐标,又D在E函数上,所以代入即可求t,进而D可表示.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,CA平分∠DCB,∠ADC=∠BAC=90°. 
(1)求证:AC2=BCDC;
(2)若BC=5,DC=1,求线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B的坐标分别为(0,8),(﹣3,0),点P从点A出发,以2单位/秒的速度沿射线AO方向运动,同时点E从点B出发,以1单位/秒的速度沿射线BO方向运动,以PE为斜边构造Rt△PEC(字母按逆时针顺序),且EC=2PC,抛物线y=﹣2x2+bx+c经过点(0,4),(﹣1,﹣2),设运动时间为t秒.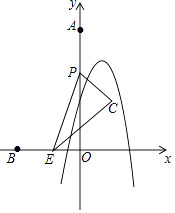
(1)求该抛物线的表达式;
(2)当t=2时,求点C的坐标;
(3)①当t<3时,求点C的坐标(用含t的代数式表示);
②在运动过程中,若点C恰好落在该抛物线上,请直接写出所有满足条件的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,已知格点△ABC和格点O.
(1)画出△ABC关于点O对称的△A′B′C′;
(2)若以点A、O、C、D为顶点的四边形是平行四边形,则点D的坐标为__.(写出所有可能的结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,且∠ABC=60°,AB=BC,△ACD的外接圆⊙O交BC于E点,连接DE并延长,交AC于P点,交AB延长线于F. 
(1)求证:CF=DB;
(2)当AD= ![]() 时,试求E点到CF的距离.
时,试求E点到CF的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为( ) 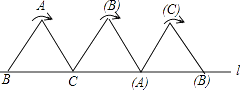
A.![]() cm
cm
B.(2+ ![]() π)cm
π)cm
C.![]() cm
cm
D.3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y= ![]() x与双曲线y=
x与双曲线y= ![]() (k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y=
(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y= ![]() (k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为 .
(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为 . 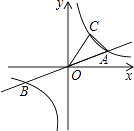
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上的一点,OC为任一射线,OD平分∠BOC,OE平分∠AOC.
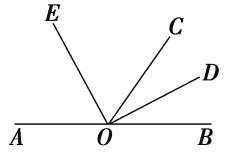
(1)指出图中∠AOD的补角和∠BOE的补角;
(2)若∠BOC=68°,求∠COD和∠EOC的度数;
(3)∠COD与∠EOC具有怎样的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只甲虫在5![]() 5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为:
5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为:![]() (+1,+3);从C到D 记为:
(+1,+3);从C到D 记为:![]() (+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.
(+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.
(1)填空:![]() 记为( , ),
记为( , ), ![]() 记为( , );
记为( , );
(2)若甲虫的行走路线为:![]() ,请你计算甲虫走过的路程.
,请你计算甲虫走过的路程.
(3)若这只甲虫去Q的行走路线依次为:A→M(+2,+2),M→N(+2,-1),N→P(-2,+3),P→Q(-1,-2),请依次在图2标出点M、N、P、Q的位置.
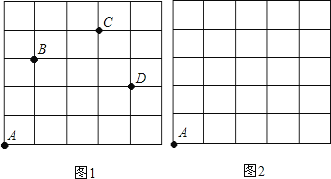
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com