
【题目】如图,在方格纸中,已知格点△ABC和格点O.
(1)画出△ABC关于点O对称的△A′B′C′;
(2)若以点A、O、C、D为顶点的四边形是平行四边形,则点D的坐标为__.(写出所有可能的结果)

科目:初中数学 来源: 题型:
【题目】某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1 000元;经粗加工后销售,每吨利润可达4 500元;经精加工后销售,每吨利润涨至7 500元.
当地一家蔬菜公司收获这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须在15天内将这批蔬菜全部销售或加工完毕,为此公司制订了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上直接销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为选择哪种方案获利最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为线段AD上一点,B为CD的中点,且AD=10cm,BD=4cm;
(1)图中共有多少条线段?写出这些线段;
(2)求AC的长;
(3)若点E在直线AD上,且AE=3cm,求BE的长;
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
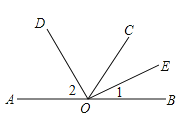
【题目】如图,O是直线AB上的一点,C是直线AB外的一点,OD是∠AOC的平分线,
OE是∠COB的平分线.
(1)已知∠1=23°,求∠2的度数;
(2)无论点C的位置如何改变,图中是否存在一个角,它的大小始终不变(∠AOB除外)?如果存在,求出这个角的度数;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】低碳生活备受关注.小明为了了解人们到某超市购物时使用购物袋的情况,利用星期日到该超市对部分购物者进行调查,并把调查结果绘制成两幅不完整的统计图.假设当天每人每次购物时都只用一个环保购物袋(可降解)或塑料购物袋(不可降解).

根据以上信息,回答下列问题:
(1)小明这次调查到的购物人数是 人次;
(2)补全两幅统计图;
(3)若当天到该超市购物者共有2000人次,请你估计使用塑料购物袋有 人次;环保购物袋有 人次;扇形C的圆心角是 度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y= ![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.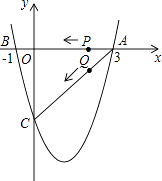
(1)求该二次函数的解析式及点C的坐标;
(2)当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E,使得以A,E,Q为顶点的三角形为等腰三角形?若存在,请求出E点坐标;若不存在,请说明理由.
(3)当P,Q运动到t秒时,△APQ沿PQ翻折,点A恰好落在抛物线上D点处,请判定此时四边形APDQ的形状,并求出D点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解决小区停车难的问题,某小区准备新建50个停车位,已知新建1个地上停车位和1个地下停车位需0.5万元,新建3个地上停车位和2个地下停车位需1.1万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)根据实际情况,该小区新建地上停车位不多于33个,且预计投资金额不超过11万元,共有几种建造方式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA. 
(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OA=5,OD=1,求线段AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com