
【题目】如图,已知直线y= ![]() x与双曲线y=
x与双曲线y= ![]() (k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y=
(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y= ![]() (k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为 .
(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为 . 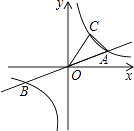
【答案】(2,4)或(8,1)
【解析】解:∵点B(﹣4,﹣2)在双曲线y= ![]() 上, ∴
上, ∴ ![]() =﹣2,
=﹣2,
∴k=8,
根据中心对称性,点A、B关于原点对称,
所以,A(4,2),
如图,过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,设点C的坐标为(a, ![]() ),
),
若S△AOC=S△COF+S梯形ACFE﹣S△AOE ,
= ![]() ×8+
×8+ ![]() ×(2+
×(2+ ![]() )(4﹣a)﹣
)(4﹣a)﹣ ![]() ×8,
×8,
=4+ ![]() ﹣4,
﹣4,
= ![]() ,
,
∵△AOC的面积为6,
∴ ![]() =6,
=6,
整理得,a2+6a﹣16=0,
解得a1=2,a2=﹣8(舍去),
∴ ![]() =
= ![]() =4,
=4,
∴点C的坐标为(2,4).
若S△AOC=S△AOE+S梯形ACFE﹣S△COF= ![]() ,
,
∴ ![]() =6,
=6,
解得:a=8或a=﹣2(舍去)
∴点C的坐标为(8,1).
所以答案是:(2,4)或(8,1).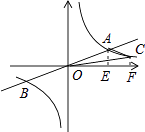


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,过点A作⊙O的切线与直径CD的延长线交于点E,已知AE=AC. 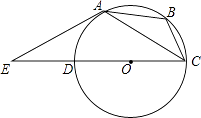
(1)求∠B的度数;
(2)若ED=1,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
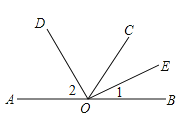
【题目】如图,O是直线AB上的一点,C是直线AB外的一点,OD是∠AOC的平分线,
OE是∠COB的平分线.
(1)已知∠1=23°,求∠2的度数;
(2)无论点C的位置如何改变,图中是否存在一个角,它的大小始终不变(∠AOB除外)?如果存在,求出这个角的度数;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y= ![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.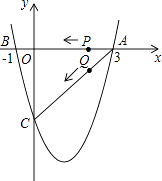
(1)求该二次函数的解析式及点C的坐标;
(2)当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E,使得以A,E,Q为顶点的三角形为等腰三角形?若存在,请求出E点坐标;若不存在,请说明理由.
(3)当P,Q运动到t秒时,△APQ沿PQ翻折,点A恰好落在抛物线上D点处,请判定此时四边形APDQ的形状,并求出D点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三角形ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).
(1)三角形A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标.
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解决小区停车难的问题,某小区准备新建50个停车位,已知新建1个地上停车位和1个地下停车位需0.5万元,新建3个地上停车位和2个地下停车位需1.1万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)根据实际情况,该小区新建地上停车位不多于33个,且预计投资金额不超过11万元,共有几种建造方式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并计算:已知线段AB=2 cm,延长线段AB至点C,使得2BC=AB,再反向延长AC至点D,使得AD=AC.
(1)准确地画出图形,并标出相应的字母;
(2)线段DC的中点是哪个?线段AB的长是线段DC长的几分之几?
(3)求出线段BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( ) 
A.πcm2
B.![]() πcm2
πcm2
C.![]() cm2
cm2
D.![]() cm2
cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级某班同学为了了解2012年某居委会家庭月均用水情况,随机调查了该居委会部分家庭,并将调查数据进行如下调整:
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | a | 0.24 |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | 0.08 |
25<x≤30 | 2 | 0.04 |
请解答以下问题:
(1)频数分布表中a= ,把频数分布直方图补充完整;
(2)求该居委会用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该居委会有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com