
【题目】如图,P是AB为直径的半圆周上一点,点C在∠PAB的平分线上,且CB⊥AB于B,PB交AC于E,若AB=4,BE=2,则PE的长为 . 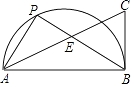
【答案】![]()
【解析】解:∵∠PAE=∠CAB,∠CAB+∠C=∠PAE+∠PEA,
∴∠PEA=∠C.
∵∠PEA=∠CEB,
∴∠C=∠CEB,
∴CB=BE=2= ![]() AB.
AB.
设PE=x,PA=2x.
(x+2)2+(2x)2=16,
解得:x= ![]() 或﹣2(舍去).
或﹣2(舍去).
则PE= ![]() .
.
故答案是: ![]() .
.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=10,BD=9,求△AED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y= ![]() x2﹣
x2﹣ ![]() x﹣3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为
x﹣3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣4ax+3a(a>0),与y轴交于点A,在x轴的正半轴上取一点B,使OB=2OA,抛物线的对称轴与抛物线交于点C,与x轴交于点D,与直线AB交于点E,连接BC.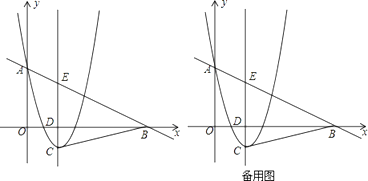
(1)求点B,C的坐标(用含a的代数式表示);
(2)若△BCD与△BDE相似,求a的值;
(3)连接OE,记△OBE的外心为M,点M到直线AB的距离记为h,请探究h的值是否会随着a的变化而变化?如果变化,请写出h的取值范围;如果不变,请求出h的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中,装有10个红球、2个黄球、8个篮球,它们除颜色外都相同.
(1)求从袋中摸出一个球是红球的概率;
(2)现从袋中取出若干个红球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率是 ![]() ,问取出了多少个红球?
,问取出了多少个红球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进A.B两种商品共160件,其进价和售价如表:
A | B | |
进价(元/件) | 15 | 35 |
售价(元/件) | 20 | 45 |
(1)当A.B两种商品分别购进多少件时,商店计划售完这批商品后能获利1100元;
(2)若商店计划购进A种商品不少于66件,且销售完这批商品后获利多于1260元,请你帮该商店老板预算有几种购货方案?获利最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠C=90°,AC=BC= ![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ) 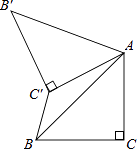
A.2﹣ ![]()
B.![]()
C.![]() ﹣1
﹣1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON为锐角.下列说法:①∠MOP=![]() ∠MON;②∠MOP=∠NOP=
∠MON;②∠MOP=∠NOP=![]() ∠MON;③∠MOP=∠NOP;④∠MON=∠MOP+∠NOP.其中,能说明射线OP一定为∠MON的平分线的有( )
∠MON;③∠MOP=∠NOP;④∠MON=∠MOP+∠NOP.其中,能说明射线OP一定为∠MON的平分线的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com