【题目】如图，在等边△ABC中，D是边AC上一点，连接BD．将△BCD绕点B逆时针旋转60°得到△BAE，连接ED．若BC=10，BD=9，求△AED的周长．
【答案】证明：∵△ABC是等边三角形，
∴AC=AB=BC=10，
∵△BAE△BCD逆时针旋旋转60°得出，
∴AE=CD，BD=BE，∠EBD=60°，
∴AE+AD=AD+CD=AC=10，
∵∠EBD=60°，BE=BD，
∴△BDE是等边三角形，
∴DE=BD=9，
∴△AED的周长=AE+AD+DE=AC+BD=19．
故答案为：19．
【解析】 本题考查的是图形旋转的性质及等边三角形的判定与性质，熟知旋转前、后的图形全等是解答此题的关键．
【考点精析】利用图形的旋转对题目进行判断即可得到答案，需要熟知每一个点都绕旋转中心沿相同方向转动了相同的角度，任意一对对应点与旋转中心的连线所成的角都是旋转角，对应点到旋转中心的距离相等．旋转的方向、角度、旋转中心是它的三要素．
科目：初中数学 来源： 题型：
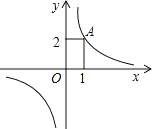
【题目】如上图，反比例函数
的图象位于第一、三象限，其中第一象限内的图象经过点A（1，2），请在第三象限内的图象上找一个你喜欢的点P，你选择的P点坐标为 ．
【答案】（-1，-2）（答案不唯一）．
【解析】试题分析：根据“第一象限内的图象经过点A（1，2）”先求出函数解析式，给x一个值负数，求出y值即可得到坐标．
试题解析：∵图象经过点A（1，2），
∴
解得k=2，
∴函数解析式为y=
，
当x=-1时，y=
=-2，
∴P点坐标为（-1，-2）（答案不唯一）．
考点：反比例函数图象上点的坐标特征．
【题型】填空题
【结束】
13
【题目】在y轴右侧且平行于y轴的直线l被反比例函数
（
）与函数
（
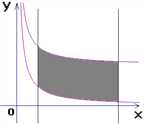
）所截，当直线l向右平移4个单位时，直线l被两函数图象所截得的线段扫过的面积为__________平方单位．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】D、E分别是不等边三角形ABC（即AB≠BC≠AC）的边AB、AC的中点．O是△ABC所在平面上的动点，连接OB、OC，点G、F分别是OB、OC的中点，顺次连接点D、G、F、E．
（1）如图，当点O在△ABC的内部时，求证：四边形DGFE是平行四边形；
（2）若四边形DGFE是菱形，则OA与BC应满足怎样的数量关系？（直接写出答案，不需要说明理由．）
查看答案和解析>>
科目：初中数学 来源： 题型：
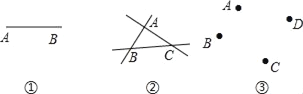
【题目】观察图①，由点A和点B可确定 条直线；
观察图②，由不在同一直线上的三点A、B和C最多能确定 条直线；
（1）动手画一画图③中经过A、B、C、D四点的所有直线，最多共可作 条直线；
（2）在同一平面内任三点不在同一直线的五个点最多能确定 条直线、n个点（n≥2）最多能确定 条直线．
查看答案和解析>>
科目：初中数学 来源： 题型：
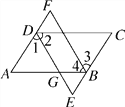
【题目】(南阳唐河县期中)如图，在ABCD中，DE平分∠ADC交AB于G，交CB的延长线于E，BF平分∠ABC交AD的延长线于F.
(1)若AD＝5，AB＝8，求GB的长；
(2)求证：∠E＝∠F.
查看答案和解析>>
科目：初中数学 来源： 题型：
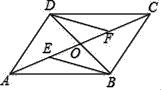
【题目】如图所示，四边形ABCD的对角线AC、BD交于点O，若OE=OF，DF∥BE．
（1）求证：△BOE≌△DOF；
（2）求证：四边形DEBF是平行四边形；
（3）若OD=OE=OF，则四边形DEBF是什么特殊的四边形，请证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知两直线L1：y=k1x+b1，L2：y=k2x+b2，若L1⊥L2，则有k1k2=﹣1．
（1）应用：已知y=2x+1与y=kx﹣1垂直，求k；
（2）直线经过A（2，3），且与y=
x+3垂直，求解析式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
